Note
Go to the end to download the full example code.
Plot Atomic Orbitals#
Visualize the wave functions (orbitals) of the hydrogen atom.
Import#
Import the applicable libraries.
Note
This example is modeled off of Matplotlib: Hydrogen Wave Function.
This example requires sympy. Install it with:
pip install sympy
from __future__ import annotations
import numpy as np
import pyvista as pv
from pyvista import examples
Generate the Dataset#
Generate the dataset by evaluating the analytic hydrogen wave function from
sympy.
See Hydrogen atom for more details.
This dataset evaluates this function for the hydrogen orbital \(3d_{xy}\), with the following quantum numbers:
Principal quantum number:
n=3Azimuthal quantum number:
l=2Magnetic quantum number:
m=-2
grid = examples.load_hydrogen_orbital(3, 2, -2)
grid
Plot the Orbital#
Plot the orbital using add_volume() and
using the default scalars contained in grid, real_wf. This way we
can plot more than just the probability of the electron, but also the phase
of the electron wave function.
Note
Since the real value of evaluated wave function for this orbital varies
between [-<value>, <value>], we cannot use the default opacity
opacity='linear'. Instead, we use [1, 0, 1] since we would like
the opacity to be proportional to the absolute value of the scalars.
pl = pv.Plotter()
vol = pl.add_volume(grid, cmap='magma', opacity=[1, 0, 1])
vol.prop.interpolation_type = 'linear'
pl.camera.zoom(2)
pl.show_axes()
pl.show()
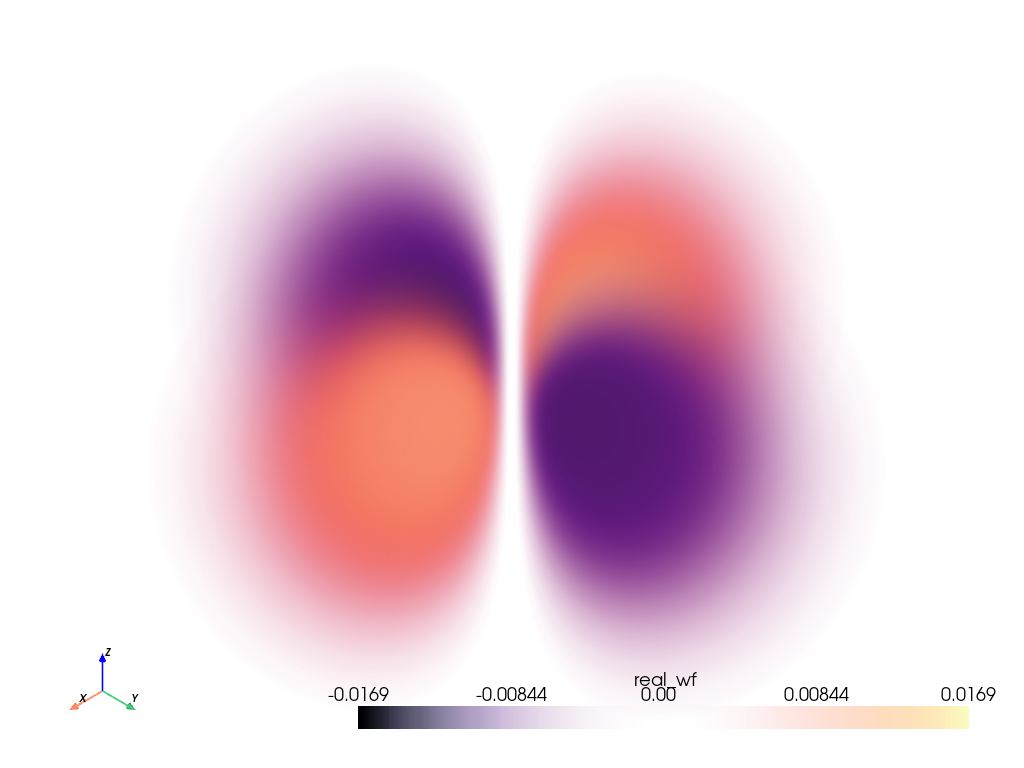
Plot the Orbital Contours as an Isosurface#
Generate the contour plot for the orbital by determining when the orbital equals 10% the maximum value of the orbital. This effectively captures the most likely locations of the electron for this orbital.
Note how we use the absolute value of the scalars when evaluating
contour() to capture where the
positive and negative phases cross eval_at.
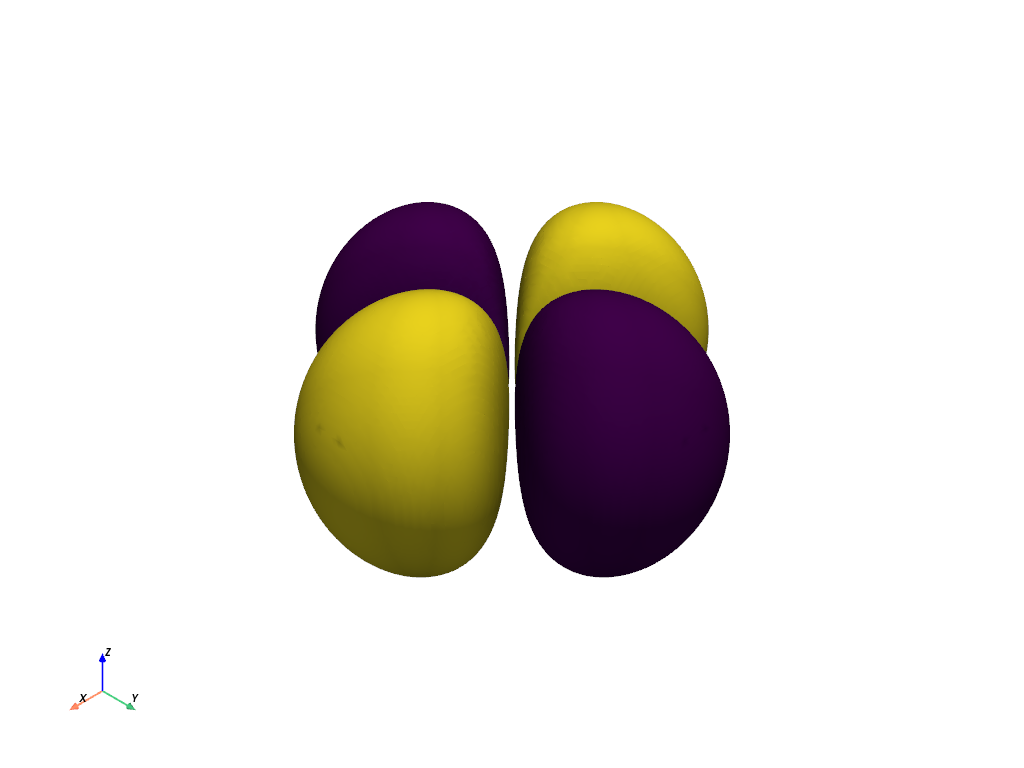
Volumetric Plot: Plot the Orbitals using RGBA#
Let’s now combine some of the best parts of the two above plots. The volumetric plot is great for showing the probability of the “electron cloud” orbitals, but the colormap doesn’t quite match reality as well as the isosurface plot.
For this example we’re going to use an RGBA colormap to tightly control the
way the orbitals are plotted. For this, the opacity will be mapped to the
probability of the electron being at a location in the grid, which we can do
by taking the absolute value squared of the orbital’s wave function. We can
set the color of the orbital based on the phase, which we can get simply
with orbital['real_wf'] < 0.
Let’s start with a simple one, the \(3p_z\) orbital.
def plot_orbital(orbital, cpos='iso', clip_plane='x'):
"""Plot an electron orbital using an RGBA colormap."""
neg_mask = orbital['real_wf'] < 0
rgba = np.zeros((orbital.n_points, 4), np.uint8)
rgba[neg_mask, 0] = 255
rgba[~neg_mask, 1] = 255
# normalize opacity
opac = np.abs(orbital['real_wf']) ** 2
opac /= opac.max()
rgba[:, -1] = opac * 255
orbital['plot_scalars'] = rgba
pl = pv.Plotter()
vol = pl.add_volume(
orbital,
scalars='plot_scalars',
)
vol.prop.interpolation_type = 'linear'
if clip_plane:
pl.add_volume_clip_plane(
vol,
normal=clip_plane,
normal_rotation=False,
)
pl.camera_position = cpos
pl.camera.zoom(1.5)
pl.show_axes()
return pl.show()
hydro_orbital = examples.load_hydrogen_orbital(3, 1, 0)
plot_orbital(hydro_orbital, clip_plane='-x')

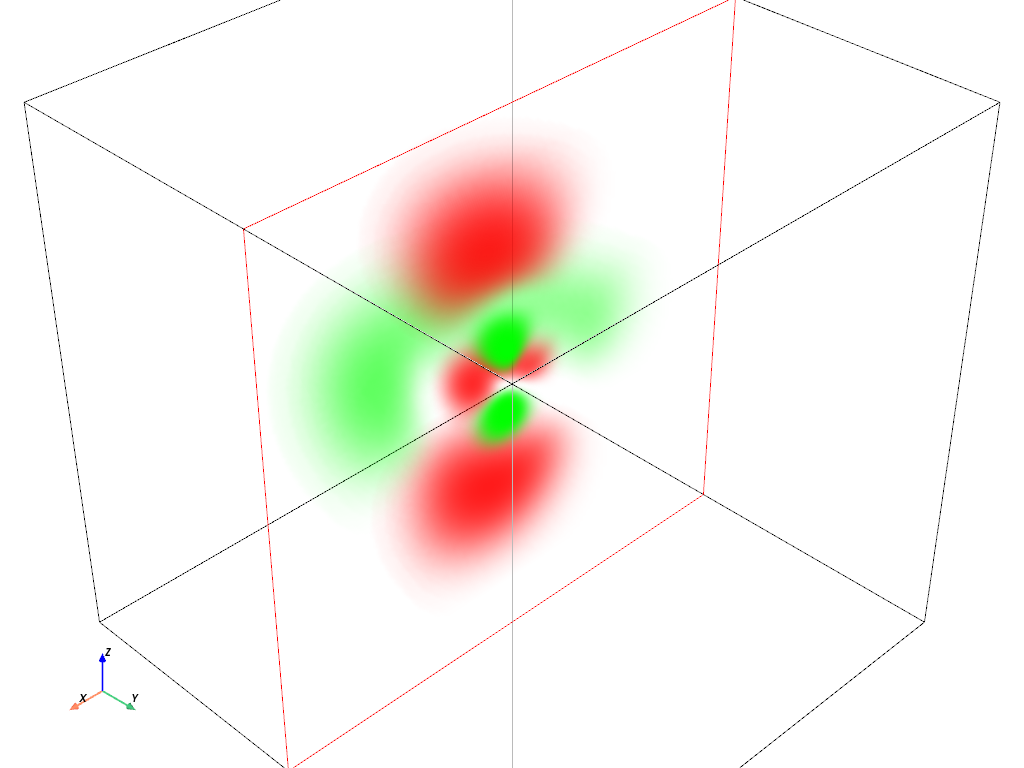
Volumetric Plot: \(4d_{z^2}\) orbital#
hydro_orbital = examples.load_hydrogen_orbital(4, 2, 0)
plot_orbital(hydro_orbital, clip_plane='-y')
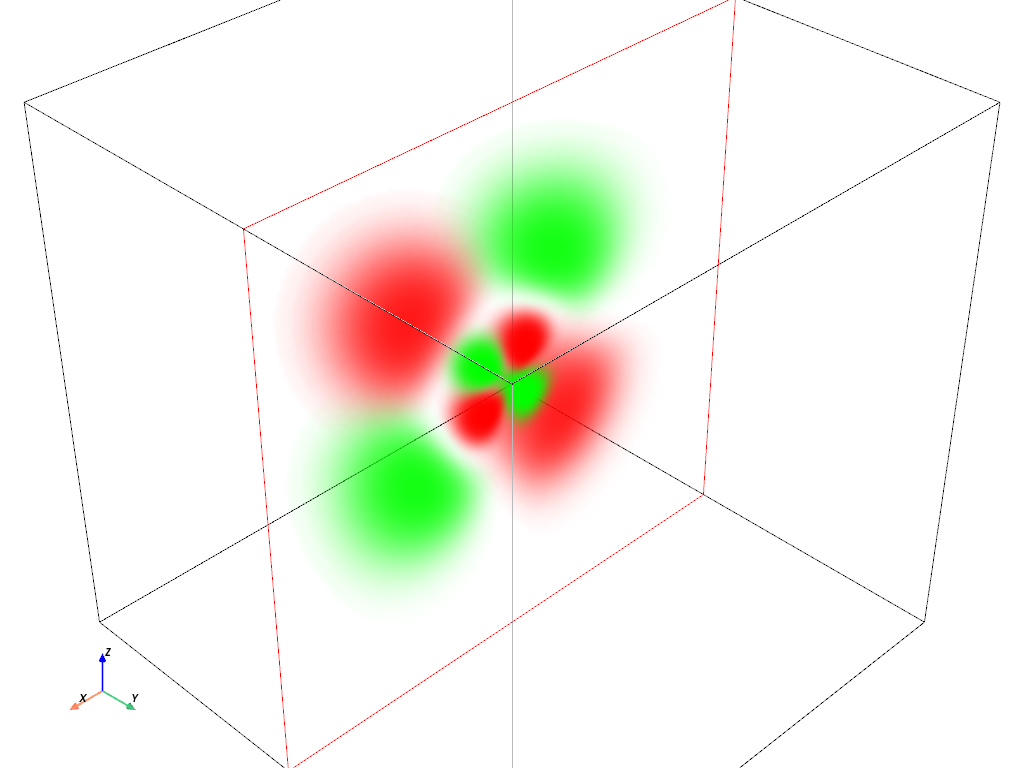
Volumetric Plot: \(4d_{xz}\) orbital#
hydro_orbital = examples.load_hydrogen_orbital(4, 2, -1)
plot_orbital(hydro_orbital, clip_plane='-y')
Plot an Orbital Using a Density Plot#
We can also plot atomic orbitals using a 3D density plot. For this, we will
use numpy.random.choice() to sample all the points of our
pyvista.ImageData based on the probability of the electron being
at that coordinate.
# Seed rng for reproducibility
rng = np.random.default_rng(seed=0)
# Generate the orbital and sample based on the square of the probability of an
# electron being within a particular volume of space.
hydro_orbital = examples.load_hydrogen_orbital(4, 2, 0, zoom_fac=0.5)
prob = np.abs(hydro_orbital['real_wf']) ** 2
prob /= prob.sum()
indices = rng.choice(hydro_orbital.n_points, 10000, p=prob)
# add a small amount of noise to these coordinates to remove the "grid like"
# structure present in the underlying ImageData
points = hydro_orbital.points[indices]
points += rng.random(points.shape) - 0.5
# Create a point cloud and add the phase as the active scalars
point_cloud = pv.PolyData(points)
point_cloud['phase'] = hydro_orbital['real_wf'][indices] < 0
# Turn the point cloud into individual spheres. We do this so we can improve
# the plot by enabling surface space ambient occlusion (SSAO)
dplot = point_cloud.glyph(
geom=pv.Sphere(theta_resolution=8, phi_resolution=8),
scale=False,
orient=False,
)
# be sure to enable SSAO here. This makes the "points" that are deeper within
# the density plot darker.
pl = pv.Plotter()
pl.add_mesh(
dplot,
smooth_shading=True,
show_scalar_bar=False,
cmap=['red', 'green'],
ambient=0.2,
)
pl.enable_ssao(radius=10)
pl.enable_anti_aliasing()
pl.camera.zoom(2)
pl.background_color = 'w'
pl.show()
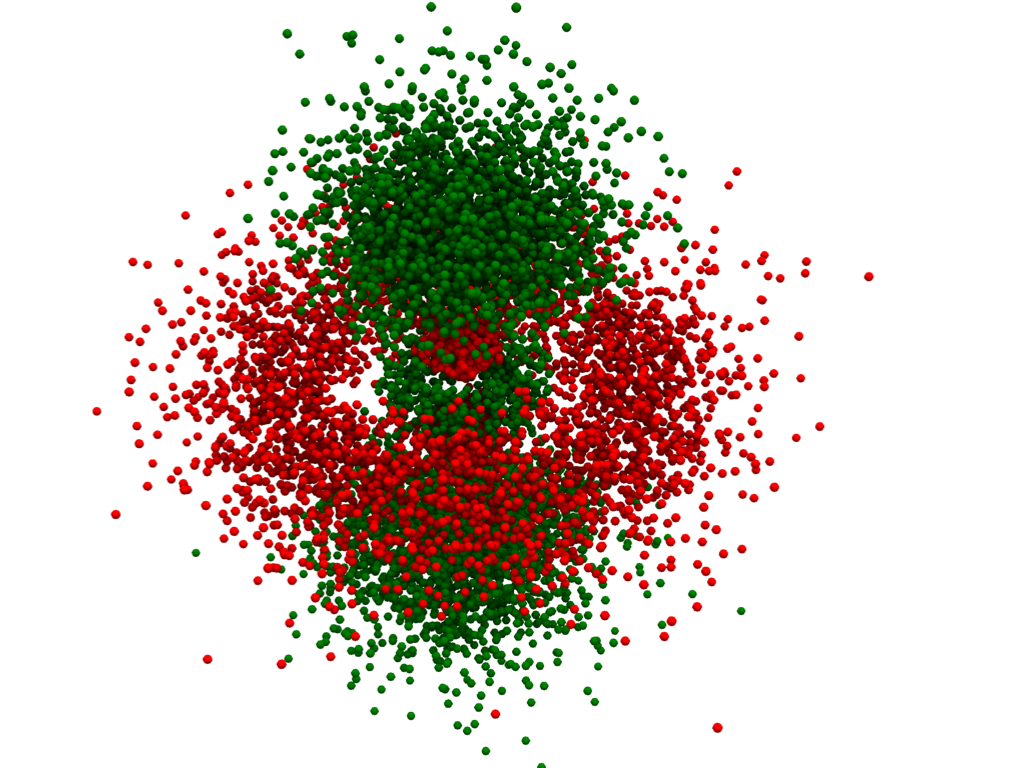
Density Plot - Gaussian Points Representation#
Finally, let’s plot the same data using the “Gaussian points” representation.
point_cloud.plot(
style='points_gaussian',
render_points_as_spheres=False,
point_size=3,
emissive=True,
background='k',
show_scalar_bar=False,
cpos='xz',
zoom=2,
)

Total running time of the script: (0 minutes 22.859 seconds)
