Note
Go to the end to download the full example code.
Creating an Unstructured Grid#
Create an irregular, unstructured grid from NumPy arrays.
This example uses pyvista.UnstructuredGrid.
from __future__ import annotations
import numpy as np
import pyvista as pv
from pyvista import CellType
An unstructured grid can be created directly from NumPy arrays. This is useful when creating a grid from scratch or copying it from another format. See vtkUnstructuredGrid for available cell types and their descriptions.
# Contains information on the points composing each cell.
# Each cell begins with the number of points in the cell and then the points
# composing the cell
cells = np.array([8, 0, 1, 2, 3, 4, 5, 6, 7, 8, 8, 9, 10, 11, 12, 13, 14, 15])
# cell type array. Contains the cell type of each cell
cell_type = np.array([CellType.HEXAHEDRON, CellType.HEXAHEDRON])
# in this example, each cell uses separate points
cell1 = np.array(
[
[0, 0, 0],
[1, 0, 0],
[1, 1, 0],
[0, 1, 0],
[0, 0, 1],
[1, 0, 1],
[1, 1, 1],
[0, 1, 1],
],
)
cell2 = np.array(
[
[0, 0, 2],
[1, 0, 2],
[1, 1, 2],
[0, 1, 2],
[0, 0, 3],
[1, 0, 3],
[1, 1, 3],
[0, 1, 3],
],
)
# points of the cell array
points = np.vstack((cell1, cell2)).astype(float)
# create the unstructured grid directly from the numpy arrays
grid = pv.UnstructuredGrid(cells, cell_type, points)
# For cells of fixed sizes (like the mentioned Hexahedra), it is also possible to use the
# simplified dictionary interface. This automatically calculates the cell array.
# Note that for mixing with additional cell types, just the appropriate key needs to be
# added to the dictionary.
cells_hex = np.arange(16).reshape([2, 8])
# = np.array([[0, 1, 2, 3, 4, 5, 6, 7], [8, 9, 10, 11, 12, 13, 14, 15]])
grid = pv.UnstructuredGrid({CellType.HEXAHEDRON: cells_hex}, points)
# plot the grid (and suppress the camera position output)
_ = grid.plot(show_edges=True)

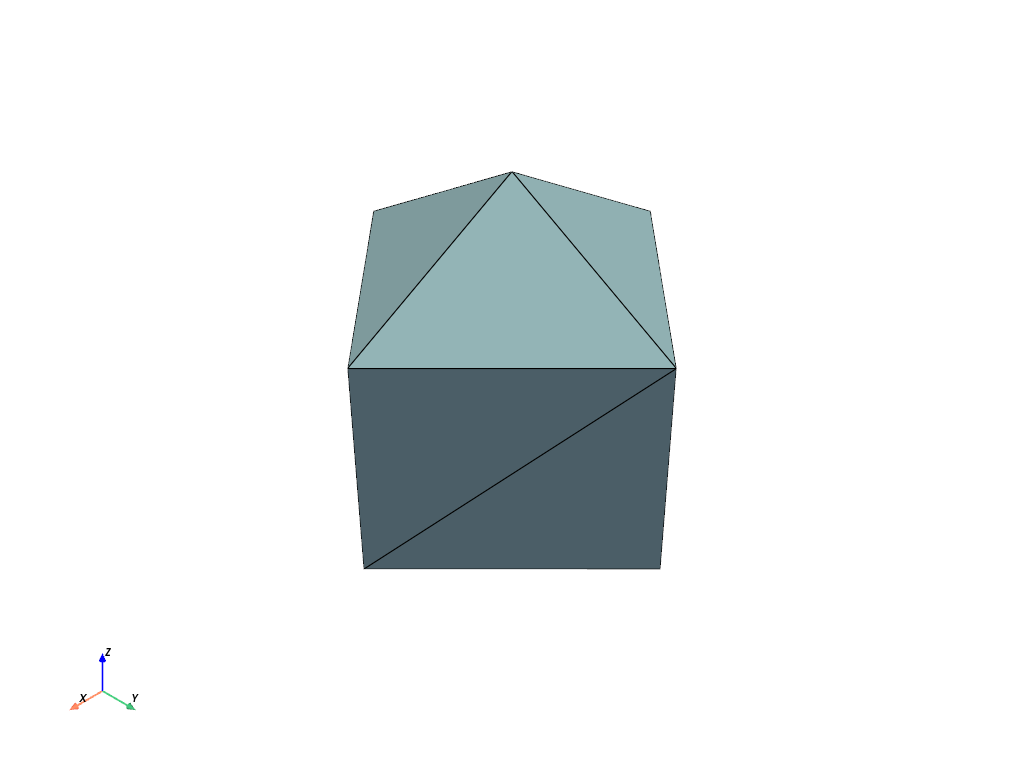
Tetrahedral Grid#
Here is how we can create an unstructured tetrahedral grid.
# There are 10 cells here, each cell is [4, INDEX0, INDEX1, INDEX2, INDEX3]
# where INDEX is one of the corners of the tetrahedron.
#
# Note that the array does not need to be shaped like this, we could have a
# flat array, but it's easier to make out the structure of the array this way.
cells = np.array(
[
[4, 6, 5, 8, 7],
[4, 7, 3, 8, 9],
[4, 7, 3, 1, 5],
[4, 9, 3, 1, 7],
[4, 2, 6, 5, 8],
[4, 2, 6, 0, 4],
[4, 6, 2, 0, 8],
[4, 5, 2, 8, 3],
[4, 5, 3, 8, 7],
[4, 2, 6, 4, 5],
],
)
celltypes = np.full(10, fill_value=CellType.TETRA, dtype=np.uint8)
# These are the 10 points. The number of cells does not need to match the
# number of points, they just happen to in this example
points = np.array(
[
[-0.0, 0.0, -0.5],
[0.0, 0.0, 0.5],
[-0.43, 0.0, -0.25],
[-0.43, 0.0, 0.25],
[-0.0, 0.43, -0.25],
[0.0, 0.43, 0.25],
[0.43, 0.0, -0.25],
[0.43, 0.0, 0.25],
[0.0, -0.43, -0.25],
[0.0, -0.43, 0.25],
],
)
# Create and plot the unstructured grid
grid = pv.UnstructuredGrid(cells, celltypes, points)
grid.plot(show_edges=True)
For fun, let’s separate all the cells and plot out the individual cells. Shift them a little bit from the center to create an “exploded view”.
split_cells = grid.explode(0.5)
split_cells.plot(show_edges=True, ssao=True)

Total running time of the script: (0 minutes 1.479 seconds)

