Linear Cells

This example extends the Creating an Unstructured Grid example by including an explanation of linear VTK cell types and how you can create them in PyVista.

Linear cells are cells where points only occur at the edges of each cell. Non-linear cells contain additional points along the edges of the cell.

For more details regarding what a pyvista.UnstructuredGrid is, please see Point Sets.

import numpy as np

import pyvista as pv
from pyvista.examples import cells as example_cells
from pyvista.examples import plot_cell

# random generator for examples
rng = np.random.default_rng(2)

Plot an example cell

PyVista contains a simple utility to plot a single cell, which is the fundamental unit of each pyvista.UnstructuredGrid. For example, let’s plot a simple Wedge.

grid = example_cells.Wedge()
example_cells.plot_cell(grid)

This linear cell is composed of 6 points.

grid.points

pyvista_ndarray([[0. , 1. , 0. ],
                 [0. , 0. , 0. ],
                 [0. , 0.5, 0.5],
                 [1. , 1. , 0. ],
                 [1. , 0. , 0. ],
                 [1. , 0.5, 0.5]])

The UnstructuredGrid is also composed of a single cell and the point indices of that cell are defined in cells.

Note

The leading 6 is the number of points in the cell.

grid.cells

array([6, 0, 1, 2, 3, 4, 5])

Combine two UnstructuredGrids

We can combine two unstructured grids to create a single unstructured grid using the + operator.

Note

This is an inefficient way of creating pyvista.UnstructuredGrid objects. To see a more efficient implementation see Creating an Unstructured Grid.

grid_a = example_cells.Hexahedron()
grid_a.points += [0, 2.5, 0]

grid_b = example_cells.HexagonalPrism()

combined = grid_b + grid_a

plot_cell(combined, cpos='iso')

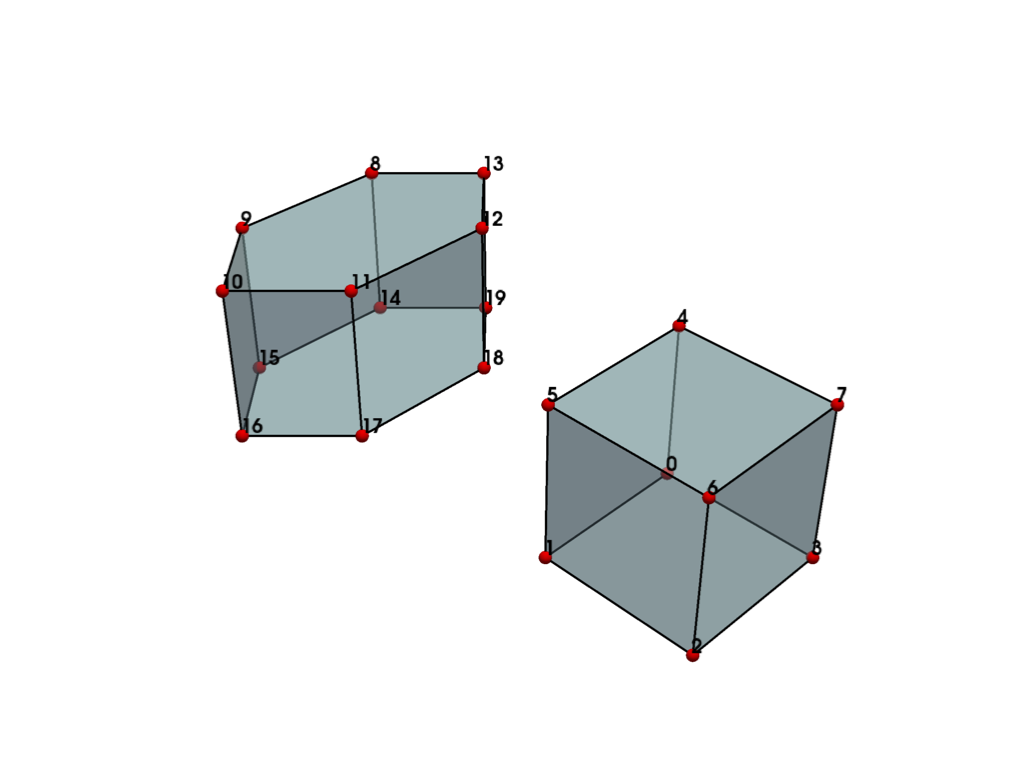
This example helps to illustrate meaning behind the cells attribute. The first cell, a hexahedron contains 8 points and the hexagonal prism contains 12 points. The cells attribute shows this along with indices composing each cell.

combined.cells

array([ 8,  0,  1,  2,  3,  4,  5,  6,  7, 12,  8,  9, 10, 11, 12, 13, 14,
       15, 16, 17, 18, 19])

Cell Types

PyVista contains the pyvista.CellType enumerator, which contains all the available VTK cell types mapped to a Python enumerator. These cell types are used when creating cells and also can be used when checking the celltypes attribute. For example combined.celltypes contains both the pv.CellType.HEXAHEDRON and pv.CellType.HEXAGONAL_PRISM cell types.

print(pv.CellType.HEXAHEDRON, pv.CellType.HEXAGONAL_PRISM)
combined.celltypes == (pv.CellType.HEXAHEDRON, pv.CellType.HEXAGONAL_PRISM)

12 16

array([ True,  True])

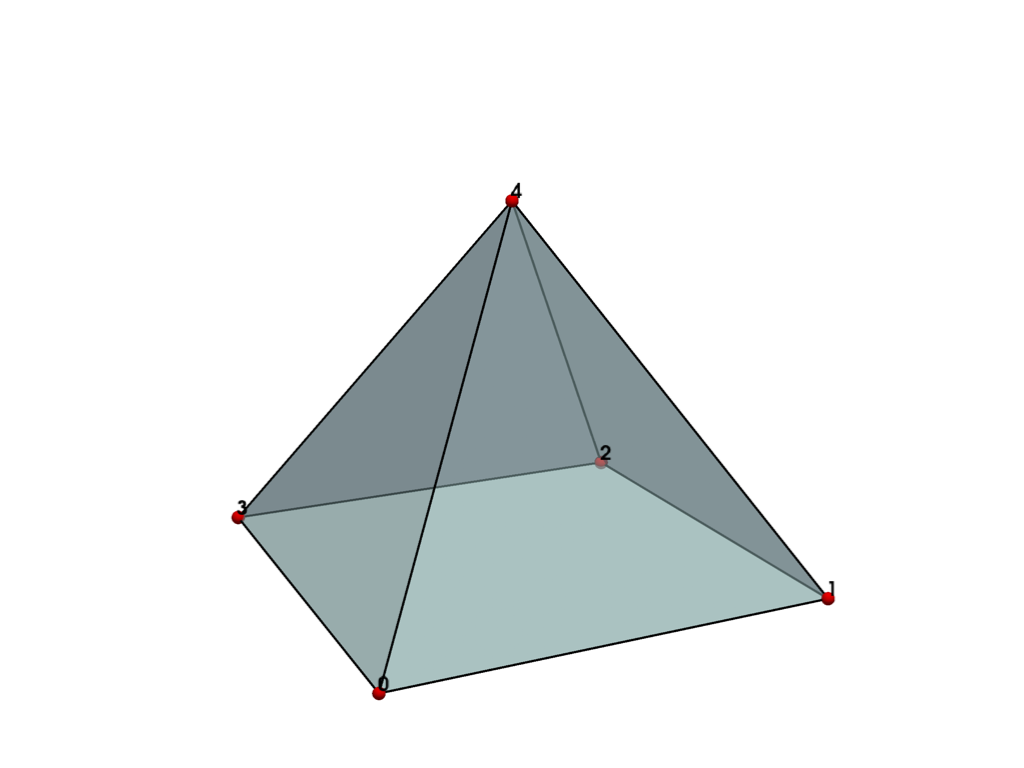
Create an UnstructuredGrid with a single linear cell

Now that you know the three main inputs of an pyvista.UnstructuredGrid, it’s quite straightforward to create an unstructured grid with a one or more cells. If you need to reference point ordering or additional, you can either read the source of cells.py or simply create a cell from the pyvista.core.cells module and inspect its attributes.

points = [
    [1.0, 1.0, 0.0],
    [-1.0, 1.0, 0.0],
    [-1.0, -1.0, 0.0],
    [1.0, -1.0, 0.0],
    [0.0, 0.0, 1.60803807],
]
cells = [len(points), *list(range(len(points)))]
pyrmaid = pv.UnstructuredGrid(cells, [pv.CellType.PYRAMID], points)
example_cells.plot_cell(pyrmaid)

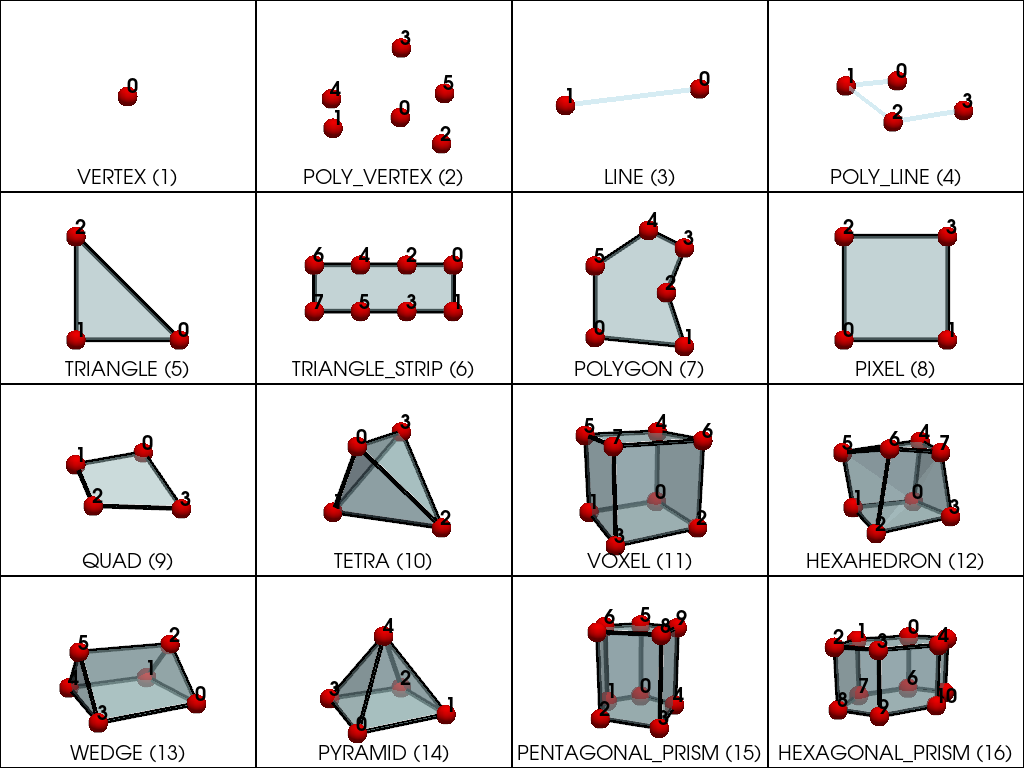
Plot all linear cell Types

Let’s create a (4, 4) pyvista.Plotter and plot all 16 linear cells in a single plot.

def add_cell_helper(pl, text, grid, subplot, cpos=None):
    """Add a single cell to a plotter with fancy plotting."""
    pl.subplot(*subplot)
    pl.add_text(text, 'lower_edge', color='k', font_size=8)
    pl.add_mesh(grid, opacity=0.5, color='lightblue', line_width=5)
    edges = grid.extract_all_edges()
    if edges.n_cells:
        pl.add_mesh(grid.extract_all_edges(), line_width=5, color='k')
    pl.add_points(grid, render_points_as_spheres=True, point_size=20, color='r')
    pl.add_point_labels(
        grid.points,
        range(grid.n_points),
        always_visible=True,
        fill_shape=False,
        margin=0,
        shape_opacity=0.0,
        font_size=20,
        text_color='k',
    )
    if cpos is None:
        pl.camera.azimuth = 20
        pl.camera.elevation = -20
    else:
        pl.camera_position = cpos
    pl.camera.zoom(0.8)


pl = pv.Plotter(shape=(4, 4))
add_cell_helper(pl, f'VERTEX ({pv.CellType.VERTEX})', example_cells.Vertex(), (0, 0))
add_cell_helper(pl, f'POLY_VERTEX ({pv.CellType.POLY_VERTEX})', example_cells.PolyVertex(), (0, 1))
add_cell_helper(pl, f'LINE ({pv.CellType.LINE})', example_cells.Line(), (0, 2))
add_cell_helper(pl, f'POLY_LINE ({pv.CellType.POLY_LINE})', example_cells.PolyLine(), (0, 3))

add_cell_helper(
    pl,
    f'TRIANGLE ({pv.CellType.TRIANGLE})',
    example_cells.Triangle(),
    (1, 0),
    cpos='xy',
)
add_cell_helper(
    pl,
    f'TRIANGLE_STRIP ({pv.CellType.TRIANGLE_STRIP})',
    example_cells.TriangleStrip().rotate_z(90, inplace=False),
    (1, 1),
    cpos='xy',
)
add_cell_helper(pl, f'POLYGON ({pv.CellType.POLYGON})', example_cells.Polygon(), (1, 2), cpos='xy')
add_cell_helper(pl, f'PIXEL ({pv.CellType.PIXEL})', example_cells.Pixel(), (1, 3), cpos='xy')

# make irregular
quad_grid = example_cells.Quadrilateral()
quad_grid.points += rng.random((4, 3)) * 0.5

add_cell_helper(pl, f'QUAD ({pv.CellType.QUAD})', quad_grid, (2, 0))
add_cell_helper(pl, f'TETRA ({pv.CellType.TETRA})', example_cells.Tetrahedron(), (2, 1))
add_cell_helper(pl, f'VOXEL ({pv.CellType.VOXEL})', example_cells.Voxel(), (2, 2))

# make irregular
hex_grid = example_cells.Hexahedron()
hex_grid.points += rng.random((8, 3)) * 0.4
add_cell_helper(pl, f'HEXAHEDRON ({pv.CellType.HEXAHEDRON})', hex_grid, (2, 3))

add_cell_helper(pl, f'WEDGE ({pv.CellType.WEDGE})', example_cells.Wedge(), (3, 0))
add_cell_helper(pl, f'PYRAMID ({pv.CellType.PYRAMID})', example_cells.Pyramid(), (3, 1))
add_cell_helper(
    pl,
    f'PENTAGONAL_PRISM ({pv.CellType.PENTAGONAL_PRISM})',
    example_cells.PentagonalPrism(),
    (3, 2),
)
add_cell_helper(
    pl,
    f'HEXAGONAL_PRISM ({pv.CellType.HEXAGONAL_PRISM})',
    example_cells.HexagonalPrism(),
    (3, 3),
)

pl.background_color = 'w'
pl.show()