Note
Go to the end to download the full example code.
Computing Surface Normals#
Compute normals on a surface.
from __future__ import annotations
import numpy as np
from pyvista import examples
Computing the normals of a surface is quite easy using
pyvista.PolyData’s pyvista.PolyDataFilters.compute_normals()
method.
mesh = examples.download_topo_global()
mesh.plot(cmap="gist_earth", show_scalar_bar=False)

Now we have a surface dataset of the globe loaded - unfortunately, the
dataset shows the globe with a uniform radius which hides topographic relief.
Using pyvista.PolyDataFilters.compute_normals(), we can compute the normal
vectors on the globe at all points in the dataset, then use the values given
in the dataset to warp the surface in the normals direction to create some
exaggerated topographic relief.
# Compute the normals in-place and use them to warp the globe
mesh.compute_normals(inplace=True) # this activates the normals as well
# Now use those normals to warp the surface
warp = mesh.warp_by_scalar(factor=0.5e-5)
# And let's see it
warp.plot(cmap="gist_earth", show_scalar_bar=False)

We could also use face/cell normals to extract all the faces of a mesh facing a general direction. In the following snippet, we take a mesh, compute the normals along its cell faces, and extract the faces that face upward.
mesh = examples.download_nefertiti()
# Compute normals
mesh.compute_normals(cell_normals=True, point_normals=False, inplace=True)
# Get list of cell IDs that meet condition
ids = np.arange(mesh.n_cells)[mesh['Normals'][:, 2] > 0.0]
# Extract those cells
top = mesh.extract_cells(ids)
cpos = [
(-834.3184529757553, -918.4677714398535, 236.5468795300025),
(11.03829376004883, -13.642289291587957, -35.91218884207208),
(0.19212361465657216, 0.11401076390090074, 0.9747256344254143),
]
top.plot(cpos=cpos, color=True)
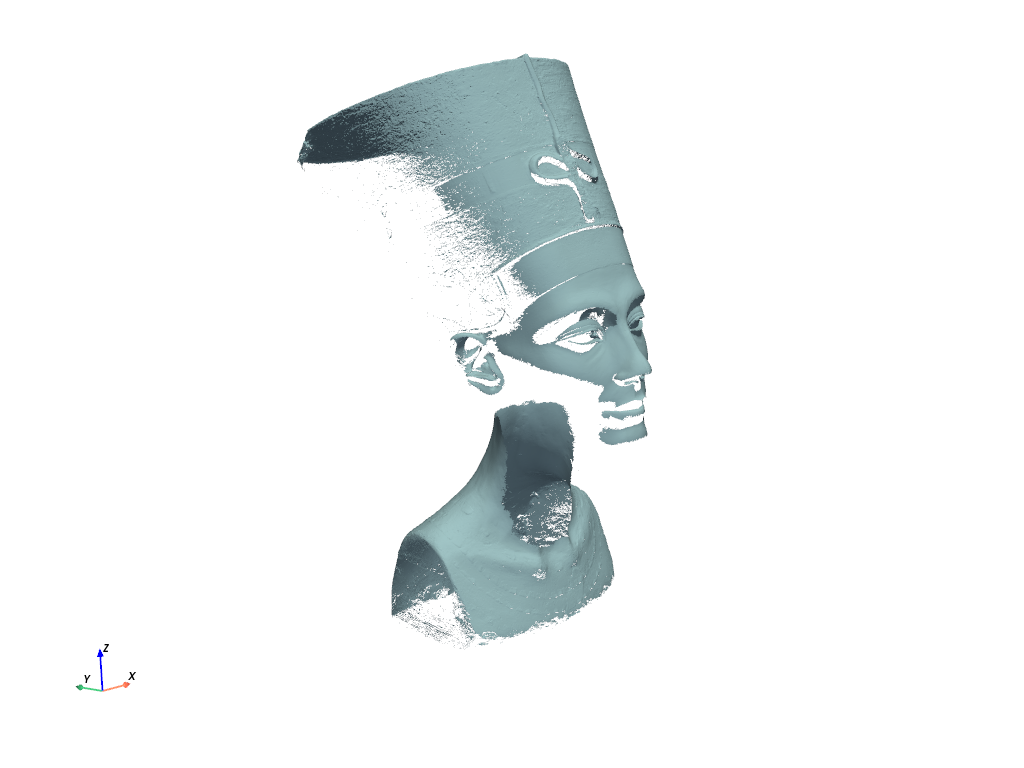
Total running time of the script: (0 minutes 49.282 seconds)
