Compute Gradients of a Field#

Estimate the gradient of a scalar or vector field in a data set.

The ordering for the output gradient tuple will be {du/dx, du/dy, du/dz, dv/dx, dv/dy, dv/dz, dw/dx, dw/dy, dw/dz} for an input array {u, v, w}.

Showing the pyvista.DataSetFilters.compute_derivative() filter.

from __future__ import annotations

import numpy as np

import pyvista as pv
from pyvista import examples

# A vtkStructuredGrid - but could be any mesh type
mesh = examples.download_carotid()
mesh

Header

Data Arrays

ImageData	Information
N Cells	158400
N Points	167580
X Bounds	1.000e+02, 1.750e+02
Y Bounds	8.000e+01, 1.280e+02
Z Bounds	1.000e+00, 4.500e+01
Dimensions	76, 49, 45
Spacing	1.000e+00, 1.000e+00, 1.000e+00
N Arrays	2

Name	Field	Type	N Comp	Min	Max
scalars	Points	float32	1	0.000e+00	5.800e+02
vectors	Points	float32	3	-2.263e+01	1.662e+01

Now compute the gradients of the vectors vector field in the point data of that mesh. This is as simple as calling pyvista.DataSetFilters.compute_derivative().

mesh_g = mesh.compute_derivative(scalars="vectors")
mesh_g["gradient"]

pyvista_ndarray([[ 7.2189998e-03,  7.6569999e-03,  3.8799997e-03, ...,
                  -7.3850001e-03,  1.0060001e-03, -2.1000043e-05],
                 [ 4.2885002e-03,  9.3000010e-04, -6.5520001e-03, ...,
                  -6.1399997e-03,  3.6770001e-03,  1.1730000e-02],
                 [ 5.4014996e-03,  1.2539998e-03, -4.6510003e-03, ...,
                   3.4900010e-04,  8.0140000e-03,  8.1439996e-03],
                 ...,
                 [-6.3999998e-04, -2.6340000e-03,  6.1740000e-03, ...,
                  -4.3205000e-03, -1.2229999e-03, -1.8960000e-03],
                 [-1.5900000e-03, -3.4460002e-03,  4.1279998e-03, ...,
                  -2.9000000e-03, -5.9960000e-03, -5.8140000e-03],
                 [-9.1199996e-04, -4.0670000e-03, -1.5819999e-03, ...,
                  -2.4759998e-03, -8.5290000e-03, -5.3939996e-03]],
                dtype=float32)

Note

You can also use pyvista.DataSetFilters.compute_derivative() for computing other derivative based quantities, such as divergence, vorticity, and Q-criterion. See function documentation for options.

mesh_g["gradient"] is an N by 9 NumPy array of the gradients, so we could make a dictionary of NumPy arrays of the gradients like:

def gradients_to_dict(arr):
    """A helper method to label the gradients into a dictionary."""
    keys = np.array(
        ["du/dx", "du/dy", "du/dz", "dv/dx", "dv/dy", "dv/dz", "dw/dx", "dw/dy", "dw/dz"],
    )
    keys = keys.reshape((3, 3))[:, : arr.shape[1]].ravel()
    return dict(zip(keys, mesh_g["gradient"].T))


gradients = gradients_to_dict(mesh_g["gradient"])
gradients

{np.str_('du/dx'): pyvista_ndarray([ 0.007219 ,  0.0042885,  0.0054015, ..., -0.00064  ,
                 -0.00159  , -0.000912 ], dtype=float32), np.str_('du/dy'): pyvista_ndarray([ 0.007657,  0.00093 ,  0.001254, ..., -0.002634,
                 -0.003446, -0.004067], dtype=float32), np.str_('du/dz'): pyvista_ndarray([ 0.00388 , -0.006552, -0.004651, ...,  0.006174,
                  0.004128, -0.001582], dtype=float32), np.str_('dv/dx'): pyvista_ndarray([-7.5999997e-04, -1.0585000e-03, -2.9600000e-03, ...,
                 -1.9554999e-03,  9.9999888e-06,  2.6600000e-03],
                dtype=float32), np.str_('dv/dy'): pyvista_ndarray([ 0.000226, -0.00503 , -0.003388, ..., -0.0059  ,
                 -0.008274, -0.000512], dtype=float32), np.str_('dv/dz'): pyvista_ndarray([-0.006821, -0.000382,  0.006909, ..., -0.001991,
                 -0.003061, -0.00189 ], dtype=float32), np.str_('dw/dx'): pyvista_ndarray([-0.007385 , -0.00614  ,  0.000349 , ..., -0.0043205,
                 -0.0029   , -0.002476 ], dtype=float32), np.str_('dw/dy'): pyvista_ndarray([ 0.001006,  0.003677,  0.008014, ..., -0.001223,
                 -0.005996, -0.008529], dtype=float32), np.str_('dw/dz'): pyvista_ndarray([-2.1000043e-05,  1.1730000e-02,  8.1439996e-03, ...,
                 -1.8960000e-03, -5.8140000e-03, -5.3939996e-03],
                dtype=float32)}

And we can add all of those components as individual arrays back to the mesh by:

mesh_g.point_data.update(gradients)
mesh_g

Header

Data Arrays

ImageData	Information
N Cells	158400
N Points	167580
X Bounds	1.000e+02, 1.750e+02
Y Bounds	8.000e+01, 1.280e+02
Z Bounds	1.000e+00, 4.500e+01
Dimensions	76, 49, 45
Spacing	1.000e+00, 1.000e+00, 1.000e+00
N Arrays	12

Name	Field	Type	N Comp	Min	Max
scalars	Points	float32	1	0.000e+00	5.800e+02
vectors	Points	float32	3	-2.263e+01	1.662e+01
gradient	Points	float32	9	-1.585e+01	1.536e+01
du/dx	Points	float32	1	-8.293e+00	8.336e+00
du/dy	Points	float32	1	-1.084e+01	8.334e+00
du/dz	Points	float32	1	-8.300e+00	8.317e+00
dv/dx	Points	float32	1	-1.133e+01	1.536e+01
dv/dy	Points	float32	1	-1.585e+01	1.170e+01
dv/dz	Points	float32	1	-1.131e+01	7.459e+00
dw/dx	Points	float32	1	-8.738e+00	1.212e+01
dw/dy	Points	float32	1	-8.734e+00	8.740e+00
dw/dz	Points	float32	1	-1.124e+01	8.728e+00

keys = np.array(list(gradients.keys())).reshape(3, 3)

p = pv.Plotter(shape=keys.shape)
for (i, j), name in np.ndenumerate(keys):
    p.subplot(i, j)
    p.add_mesh(mesh_g.contour(scalars=name), scalars=name, opacity=0.75)
    p.add_mesh(mesh_g.outline(), color="k")
p.link_views()
p.view_isometric()
p.show()

Static Scene

Interactive Scene

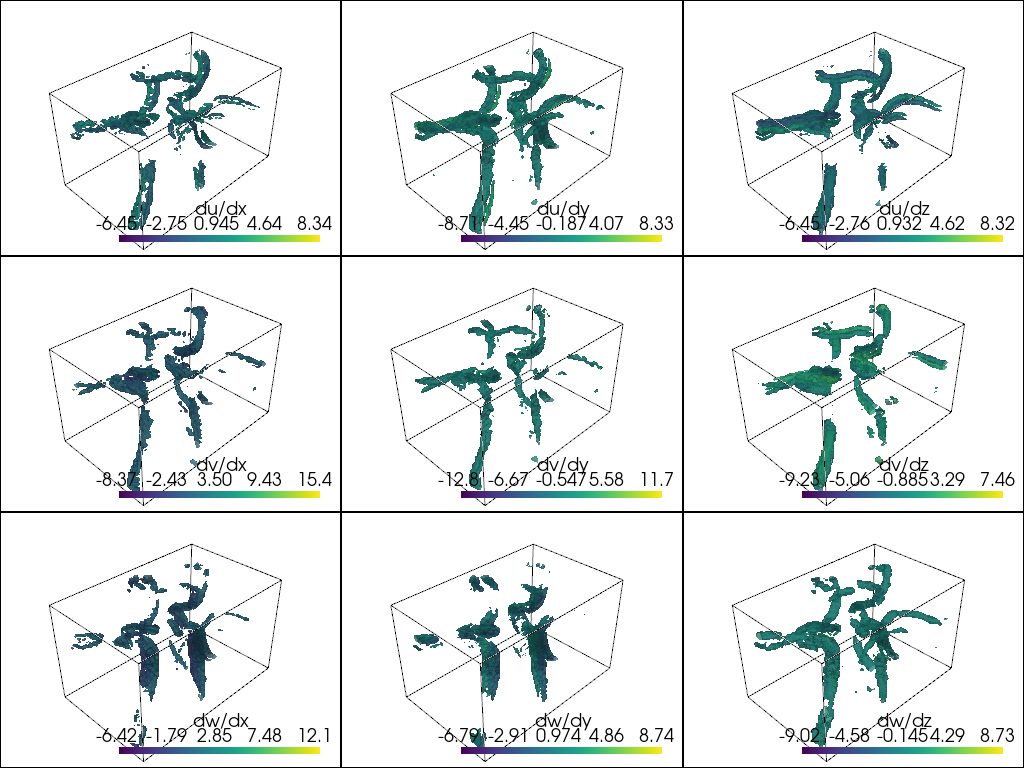
And there you have it, the gradients for a vector field. We could also do this for a scalar field like for the scalars field in the given dataset.

mesh_g = mesh.compute_derivative(scalars="scalars")

gradients = gradients_to_dict(mesh_g["gradient"])
gradients

{np.str_('du/dx'): pyvista_ndarray([-7. , -7. , -4. , ..., -0.5, -1.5, -2. ], dtype=float32), np.str_('du/dy'): pyvista_ndarray([ 0.,  5., 12., ..., -3., -1., -3.], dtype=float32), np.str_('du/dz'): pyvista_ndarray([-13.,  -8.,  -3., ...,   4.,   4.,   1.], dtype=float32)}

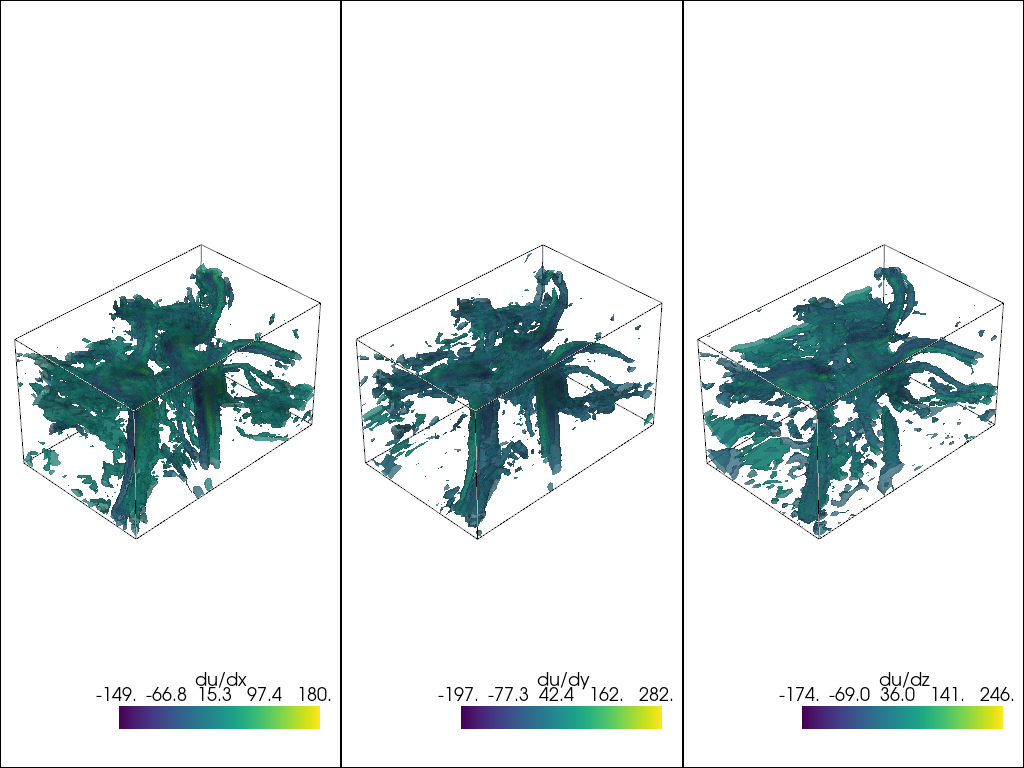
mesh_g.point_data.update(gradients)

keys = np.array(list(gradients.keys())).reshape(1, 3)

p = pv.Plotter(shape=keys.shape)

for (i, j), name in np.ndenumerate(keys):
    name = keys[i, j]
    p.subplot(i, j)
    p.add_mesh(mesh_g.contour(scalars=name), scalars=name, opacity=0.75)
    p.add_mesh(mesh_g.outline(), color="k")
p.link_views()
p.view_isometric()
p.show()

Static Scene

Interactive Scene

Total running time of the script: (0 minutes 3.495 seconds)

Gallery generated by Sphinx-Gallery