Note
Go to the end to download the full example code.
Volumetric Analysis#
Calculate mass properties such as the volume or area of datasets
from __future__ import annotations
import numpy as np
from pyvista import examples
Computing mass properties such as the volume or area of datasets in PyVista
is quite easy using the pyvista.DataSetFilters.compute_cell_sizes()
filter and the pyvista.DataSet.volume property on all PyVista meshes.
Let’s get started with a simple gridded mesh:
# Load a simple example mesh
dataset = examples.load_uniform()
dataset.set_active_scalars("Spatial Cell Data")
(<FieldAssociation.CELL: 1>, pyvista_ndarray([ 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 1., 2., 3., 4., 5., 6., 7., 8.,
0., 2., 4., 6., 8., 10., 12., 14., 16.,
0., 3., 6., 9., 12., 15., 18., 21., 24.,
0., 4., 8., 12., 16., 20., 24., 28., 32.,
0., 5., 10., 15., 20., 25., 30., 35., 40.,
0., 6., 12., 18., 24., 30., 36., 42., 48.,
0., 7., 14., 21., 28., 35., 42., 49., 56.,
0., 8., 16., 24., 32., 40., 48., 56., 64.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 2., 4., 6., 8., 10., 12., 14., 16.,
0., 4., 8., 12., 16., 20., 24., 28., 32.,
0., 6., 12., 18., 24., 30., 36., 42., 48.,
0., 8., 16., 24., 32., 40., 48., 56., 64.,
0., 10., 20., 30., 40., 50., 60., 70., 80.,
0., 12., 24., 36., 48., 60., 72., 84., 96.,
0., 14., 28., 42., 56., 70., 84., 98., 112.,
0., 16., 32., 48., 64., 80., 96., 112., 128.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 3., 6., 9., 12., 15., 18., 21., 24.,
0., 6., 12., 18., 24., 30., 36., 42., 48.,
0., 9., 18., 27., 36., 45., 54., 63., 72.,
0., 12., 24., 36., 48., 60., 72., 84., 96.,
0., 15., 30., 45., 60., 75., 90., 105., 120.,
0., 18., 36., 54., 72., 90., 108., 126., 144.,
0., 21., 42., 63., 84., 105., 126., 147., 168.,
0., 24., 48., 72., 96., 120., 144., 168., 192.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 4., 8., 12., 16., 20., 24., 28., 32.,
0., 8., 16., 24., 32., 40., 48., 56., 64.,
0., 12., 24., 36., 48., 60., 72., 84., 96.,
0., 16., 32., 48., 64., 80., 96., 112., 128.,
0., 20., 40., 60., 80., 100., 120., 140., 160.,
0., 24., 48., 72., 96., 120., 144., 168., 192.,
0., 28., 56., 84., 112., 140., 168., 196., 224.,
0., 32., 64., 96., 128., 160., 192., 224., 256.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 5., 10., 15., 20., 25., 30., 35., 40.,
0., 10., 20., 30., 40., 50., 60., 70., 80.,
0., 15., 30., 45., 60., 75., 90., 105., 120.,
0., 20., 40., 60., 80., 100., 120., 140., 160.,
0., 25., 50., 75., 100., 125., 150., 175., 200.,
0., 30., 60., 90., 120., 150., 180., 210., 240.,
0., 35., 70., 105., 140., 175., 210., 245., 280.,
0., 40., 80., 120., 160., 200., 240., 280., 320.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 6., 12., 18., 24., 30., 36., 42., 48.,
0., 12., 24., 36., 48., 60., 72., 84., 96.,
0., 18., 36., 54., 72., 90., 108., 126., 144.,
0., 24., 48., 72., 96., 120., 144., 168., 192.,
0., 30., 60., 90., 120., 150., 180., 210., 240.,
0., 36., 72., 108., 144., 180., 216., 252., 288.,
0., 42., 84., 126., 168., 210., 252., 294., 336.,
0., 48., 96., 144., 192., 240., 288., 336., 384.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 7., 14., 21., 28., 35., 42., 49., 56.,
0., 14., 28., 42., 56., 70., 84., 98., 112.,
0., 21., 42., 63., 84., 105., 126., 147., 168.,
0., 28., 56., 84., 112., 140., 168., 196., 224.,
0., 35., 70., 105., 140., 175., 210., 245., 280.,
0., 42., 84., 126., 168., 210., 252., 294., 336.,
0., 49., 98., 147., 196., 245., 294., 343., 392.,
0., 56., 112., 168., 224., 280., 336., 392., 448.,
0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 8., 16., 24., 32., 40., 48., 56., 64.,
0., 16., 32., 48., 64., 80., 96., 112., 128.,
0., 24., 48., 72., 96., 120., 144., 168., 192.,
0., 32., 64., 96., 128., 160., 192., 224., 256.,
0., 40., 80., 120., 160., 200., 240., 280., 320.,
0., 48., 96., 144., 192., 240., 288., 336., 384.,
0., 56., 112., 168., 224., 280., 336., 392., 448.,
0., 64., 128., 192., 256., 320., 384., 448., 512.]))
We can then calculate the volume of every cell in the array using the
.compute_cell_sizes filter which will add arrays to the cell data of the
mesh core the volume and area by default.
# Compute volumes and areas
sized = dataset.compute_cell_sizes()
# Grab volumes for all cells in the mesh
cell_volumes = sized.cell_data["Volume"]
We can also compute the total volume of the mesh using the .volume
property:
But what if we have a dataset that we threshold with two volumetric bodies left over in one dataset? Take this for example:
threshed = dataset.threshold_percent([0.15, 0.50], invert=True)
threshed.plot(show_grid=True, cpos=[-2, 5, 3])
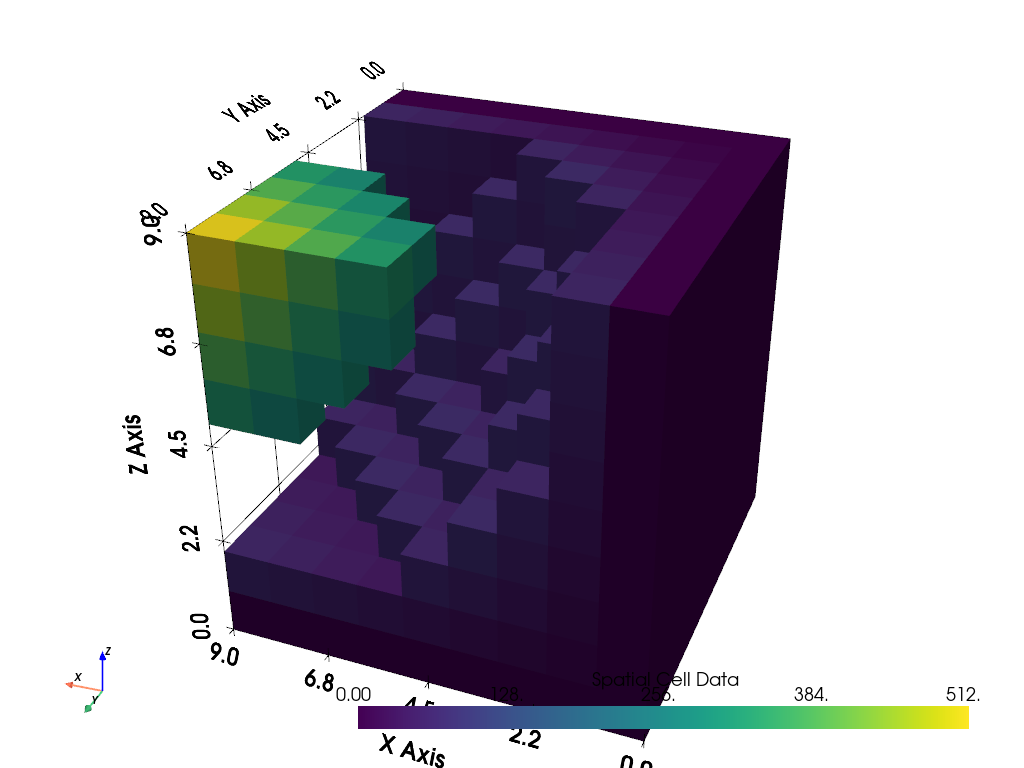
We could then assign a classification array for the two bodies, compute the cell sizes, then extract the volumes of each body. Note that there is a simpler implementation of this below in Splitting Volumes.
# Create a classifying array to ID each body
rng = dataset.get_data_range()
cval = ((rng[1] - rng[0]) * 0.20) + rng[0]
classifier = threshed.cell_data["Spatial Cell Data"] > cval
# Compute cell volumes
sizes = threshed.compute_cell_sizes()
volumes = sizes.cell_data["Volume"]
# Split volumes based on classifier and get the volumes
idx = np.argwhere(classifier)
hvol = np.sum(volumes[idx])
idx = np.argwhere(~classifier)
lvol = np.sum(volumes[idx])
print(f"Low grade volume: {lvol}")
print(f"High grade volume: {hvol}")
print(f"Original volume: {dataset.volume}")
Low grade volume: 518.0
High grade volume: 32.0
Original volume: 729.0
Or better yet, you could simply extract the largest volume from your
dataset directly by passing 'largest' to the connectivity and
specifying the scalar range of interest.
# Grab the largest connected volume within a scalar range
scalar_range = [0, 77] # Range corresponding to bottom 15% of values
largest = threshed.connectivity('largest', scalar_range=scalar_range)
# Get volume as numeric value
large_volume = largest.volume
# Display it
largest.plot(show_grid=True, cpos=[-2, 5, 3])
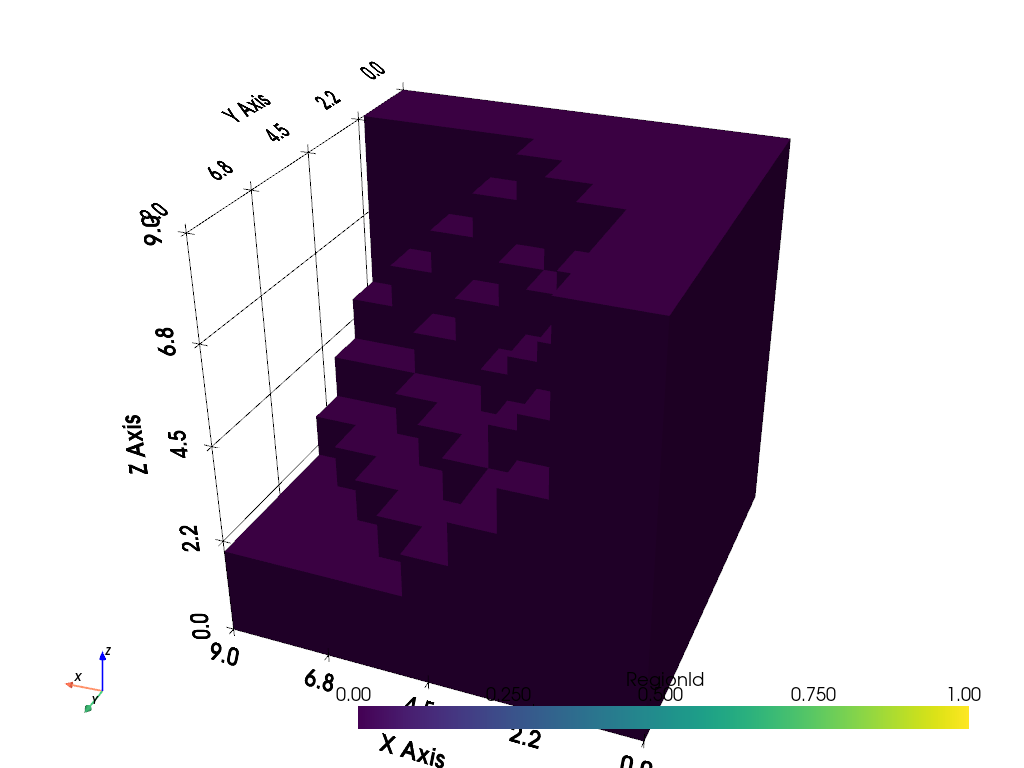
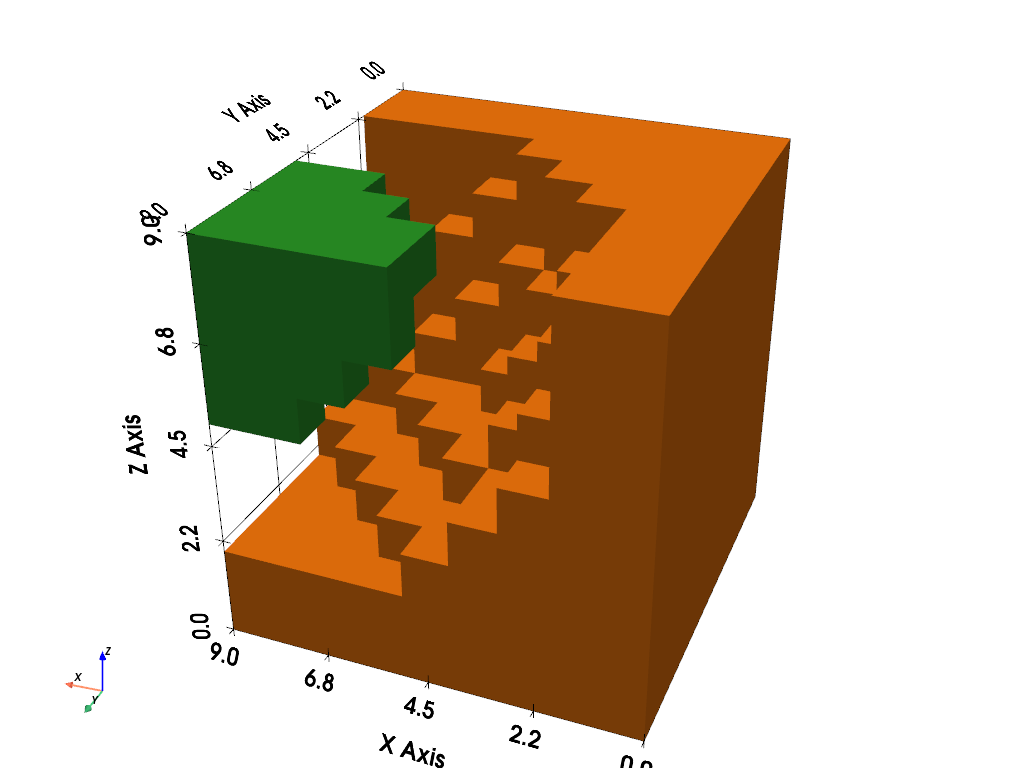
Splitting Volumes#
What if instead, we wanted to split all the different connected bodies /
volumes in a dataset like the one above? We could use the
pyvista.DataSetFilters.split_bodies() filter to extract all the
different connected volumes in a dataset into blocks in a
pyvista.MultiBlock dataset. For example, lets split the thresholded
volume in the example above:
Body 0 volume: 518.000
Body 1 volume: 32.000
bodies.plot(show_grid=True, multi_colors=True, cpos=[-2, 5, 3])
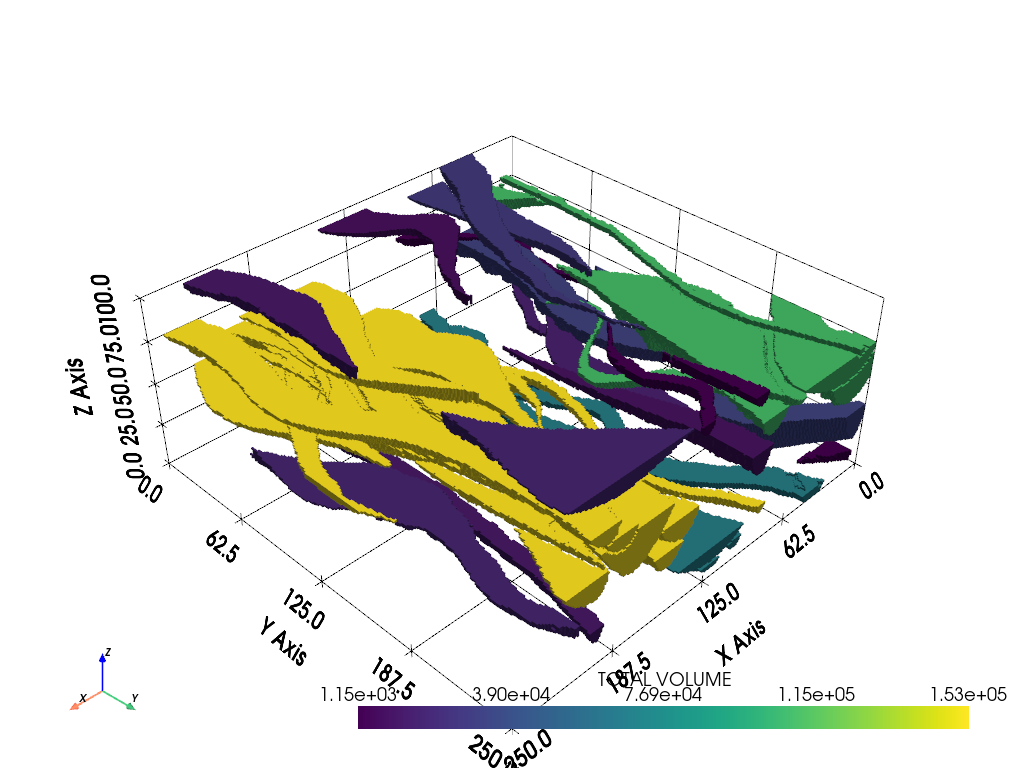
A Real Dataset#
Here is a realistic training dataset of fluvial channels in the subsurface. This will threshold the channels from the dataset then separate each significantly large body and compute the volumes for each.
Load up the data and threshold the channels:
data = examples.load_channels()
channels = data.threshold([0.9, 1.1])
Now extract all the different bodies and compute their volumes:
Print out the volumes for each body:
Body 00 volume: 152667.000
Body 01 volume: 152638.000
Body 02 volume: 108024.000
Body 03 volume: 66761.000
Body 04 volume: 32520.000
Body 05 volume: 31866.000
Body 06 volume: 27857.000
Body 07 volume: 18269.000
Body 08 volume: 18238.000
Body 09 volume: 16120.000
Body 10 volume: 12550.000
Body 11 volume: 12490.000
Body 12 volume: 9861.000
Body 13 volume: 8239.000
Body 14 volume: 5166.000
Body 15 volume: 2270.000
Body 16 volume: 2085.000
Body 17 volume: 1889.000
Body 18 volume: 1548.000
Body 19 volume: 1443.000
Body 20 volume: 1150.000
And visualize all the different volumes:
bodies.plot(scalars="TOTAL VOLUME", cmap="viridis", show_grid=True)
Total running time of the script: (0 minutes 7.289 seconds)
