pyvista.Icosphere#
- Icosphere( ) PolyData[source]#
Create an icosphere.
An icosphere is a geodesic polyhedron, which is a convex polyhedron made from triangles.
Geodesic polyhedra are constructed by subdividing faces of simpler polyhedra, and then projecting the new vertices onto the surface of a sphere. A geodesic polyhedron has straight edges and flat faces that approximate a sphere,
- Parameters:
- radius
float, default: 1.0 Radius of the icosphere.
- centersequence[
float], default: (0.0, 0.0, 0.0) Center of the icosphere.
- nsub
int, default: 3 This is the number of times each triangle of the original
pyvista.Icosahedron()is subdivided.
- radius
- Returns:
pyvista.PolyDataMesh of the icosphere.
See also
Examples
Create the icosphere and plot it with edges.
>>> import pyvista as pv >>> icosphere = pv.Icosphere() >>> icosphere.plot(show_edges=True)

Show how this icosphere was created.
>>> import numpy as np >>> icosahedron = pv.Icosahedron() >>> icosahedron.clear_data() # remove extra scalars >>> icosahedron_sub = icosahedron.subdivide(nsub=3) >>> pl = pv.Plotter(shape=(1, 3)) >>> _ = pl.add_mesh(icosahedron, show_edges=True) >>> pl.subplot(0, 1) >>> _ = pl.add_mesh(icosahedron_sub, show_edges=True) >>> pl.subplot(0, 2) >>> _ = pl.add_mesh(icosphere, show_edges=True) >>> pl.show()

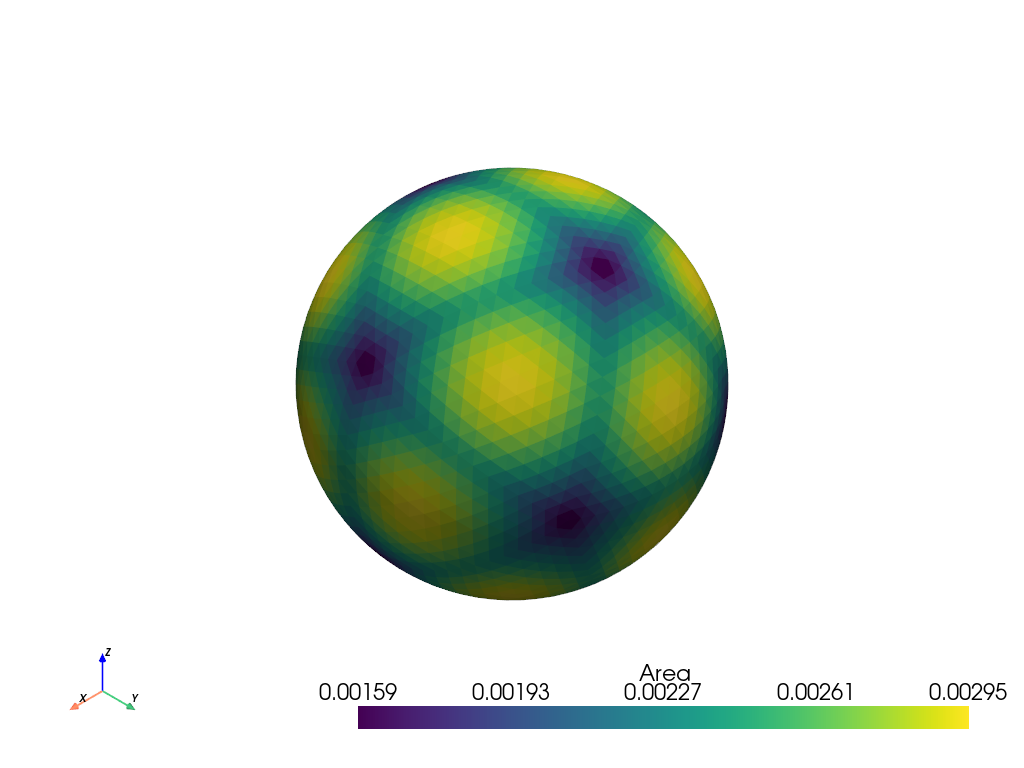
Show how the triangles are not uniform in area. This is because the ones farther from the edges from the original triangles have farther to travel to the sphere.
>>> icosphere = pv.Icosphere(nsub=4) >>> icosphere.compute_cell_sizes().plot(scalars='Area')