What is a Mesh?#
In PyVista, a mesh is any spatially referenced information and usually consists of geometrical representations of a surface or volume in 3D space. We commonly refer to any spatially referenced dataset as a mesh, so often the distinction between a mesh, a grid, and a volume can get fuzzy, but that does not matter in PyVista. If you have a dataset that is a surface mesh with 2D geometries like triangles, we call it a mesh, and if you have a dataset with 3D geometries like voxels, tetrahedra, hexahedra, etc., then we also call that a mesh. Why? Because it is simple that way.
In all spatially referenced datasets, there lies an underlying mesh structure which is the connectivity between vertices to define cells. Whether those cells are 2D or 3D is not always of importance and we’ve worked hard to make PyVista work for datasets of either or mixed geometries so that you as a user do not have to get bogged down in the nuances.
Note
This is a very high level overview of the PyVista API. For further details regarding our data model and how it relates to the underlying VTK data model, please see PyVista Data Model.
What is a Point?#
Points are the vertices of the mesh, also referred to as the Cartesian coordinates of the underlying structure. All PyVista datasets (meshes) have points and sometimes, you can have a mesh that only has points, like a point cloud.
For example, you can create a point cloud mesh using the
pyvista.PolyData class which is built for meshes that have 1D
and 2D cell types (we’ll get into what a cell is briefly).
Let’s start with a point cloud; this is a mesh type that only has vertices. You can create one by defining a 2D array of Cartesian coordinates like so:
# must have this here as our global backend may not be static
import pyvista as pv
pv.set_plot_theme('document')
pv.set_jupyter_backend('static')
pv.global_theme.window_size = [600, 400]
pv.global_theme.axes.show = False
pv.global_theme.anti_aliasing = 'fxaa'
pv.global_theme.show_scalar_bar = False
import numpy as np
import pyvista as pv
rng = np.random.default_rng(seed=0)
points = rng.random((100, 3))
mesh = pv.PolyData(points)
mesh.plot(point_size=10, style='points')

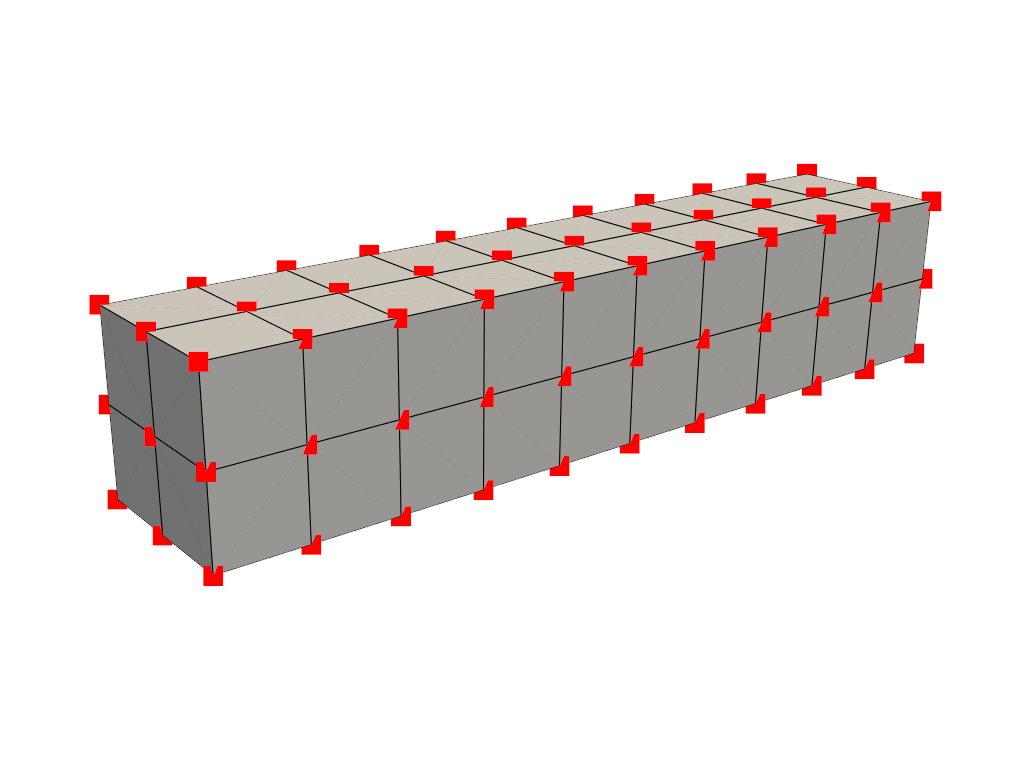
But it’s important to note that most meshes have some sort of connectivity between points such as this gridded mesh:
from pyvista import examples
mesh = examples.load_hexbeam()
cpos = pv.CameraPosition(position=(6.20, 3.00, 7.50),
focal_point=(0.16, 0.13, 2.65),
viewup=(-0.28, 0.94, -0.21))
pl = pv.Plotter()
pl.add_mesh(mesh, show_edges=True, color='white')
pl.add_points(mesh.points, color='red',
point_size=20)
pl.camera_position = cpos
pl.show()
Or this triangulated surface:
mesh = examples.download_bunny_coarse()
pl = pv.Plotter()
pl.add_mesh(mesh, show_edges=True, color='white')
pl.add_points(mesh.points, color='red',
point_size=2)
pl.camera_position = pv.CameraPosition(
position=(0.02, 0.30, 0.73),
focal_point=(0.02, 0.03, -0.022),
viewup=(-0.03, 0.94, -0.34)
)
pl.show()

What is a Cell?#
A cell is the geometry between points that defines the connectivity or topology of a mesh. In the examples above, cells are defined by the lines (edges colored in black) connecting points (colored in red). For example, a cell in the beam example is a voxel defined by the region between eight points in that mesh:
mesh = examples.load_hexbeam()
pl = pv.Plotter()
pl.add_mesh(mesh, show_edges=True, color='white')
pl.add_points(mesh.points, color='red', point_size=20)
single_cell = mesh.extract_cells(mesh.n_cells - 1)
pl.add_mesh(single_cell, color='pink', edge_color='blue',
line_width=5, show_edges=True)
pl.camera_position = pv.CameraPosition(
position=(6.20, 3.00, 7.50),
focal_point=(0.16, 0.13, 2.65),
viewup=(-0.28, 0.94, -0.21)
)
pl.show()
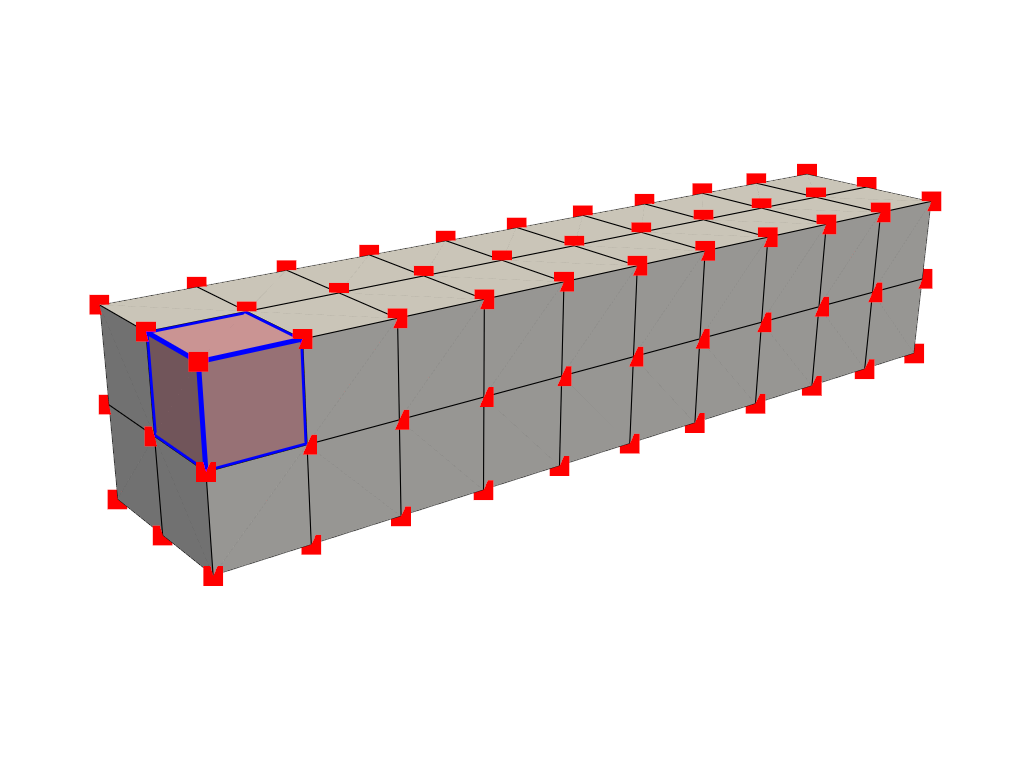
Cells aren’t limited to voxels, they could be a triangle between three points, a line between two points, or even a single point could be its own cell (but that’s a special case).
What are Attributes?#
Attributes are data values that live on either the points or cells of a mesh. In PyVista, we work with both point data and cell data and allow easy access to data dictionaries to hold arrays for attributes that live either on all points or on all cells of a mesh. These attributes can be accessed in a Dictionary-like attribute attached to any PyVista mesh accessible as one of the following:
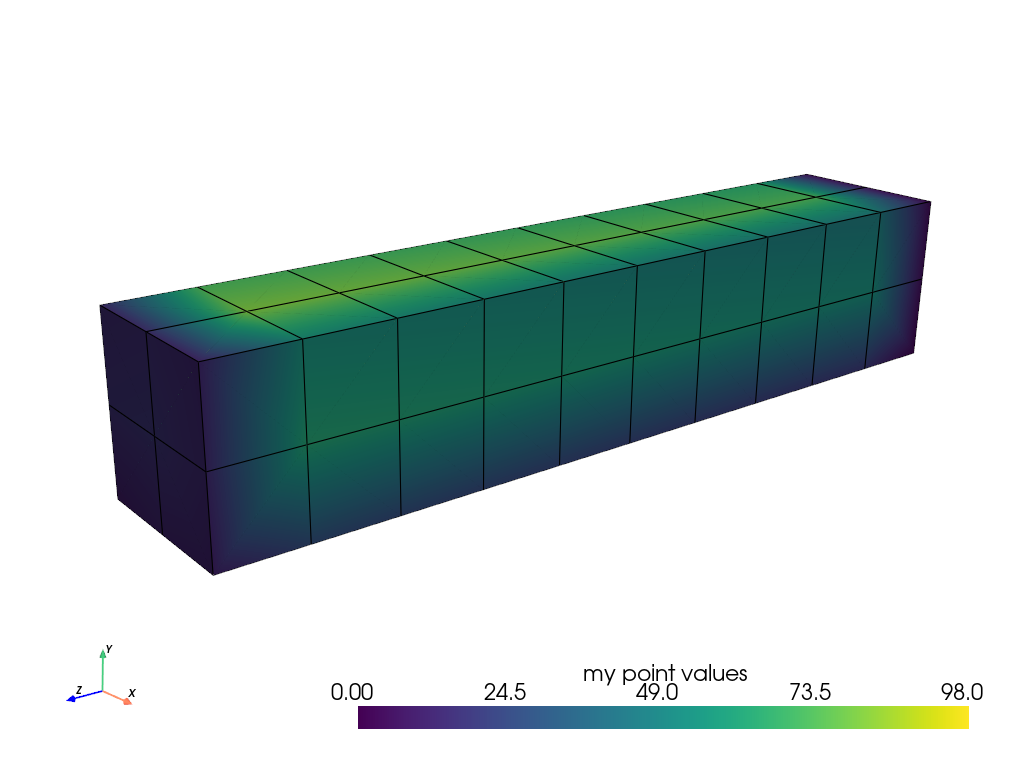
Point Data#
Point data refers to arrays of values (scalars, vectors, etc.) that live on each point of the mesh. Each element in an attribute array corresponds to a point in the mesh. Let’s create some point data for the beam mesh. When plotting, the values between points are interpolated across the cells.
mesh.point_data['my point values'] = np.arange(mesh.n_points)
mesh.plot(scalars='my point values', cpos=cpos, show_edges=True)
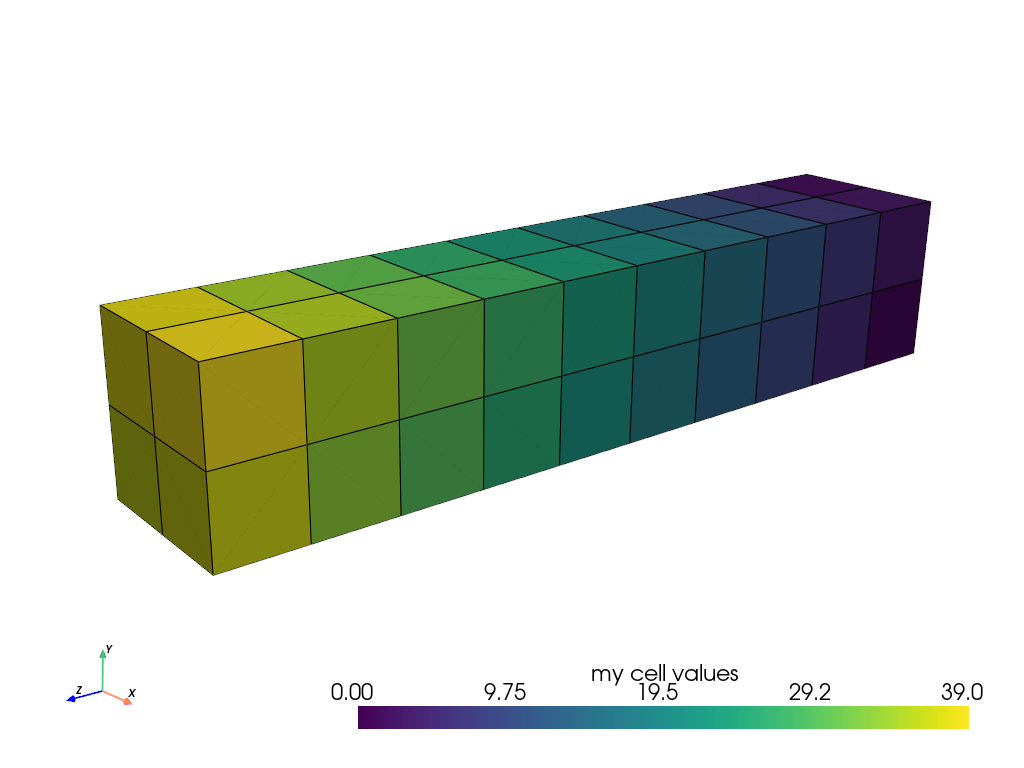
Cell Data#
Cell data refers to arrays of values (scalars, vectors, etc.) that live throughout each cell of the mesh. That is the entire cell (2D face or 3D volume) is assigned the value of that attribute.
mesh.cell_data['my cell values'] = np.arange(mesh.n_cells)
mesh.plot(scalars='my cell values', cpos=cpos, show_edges=True)
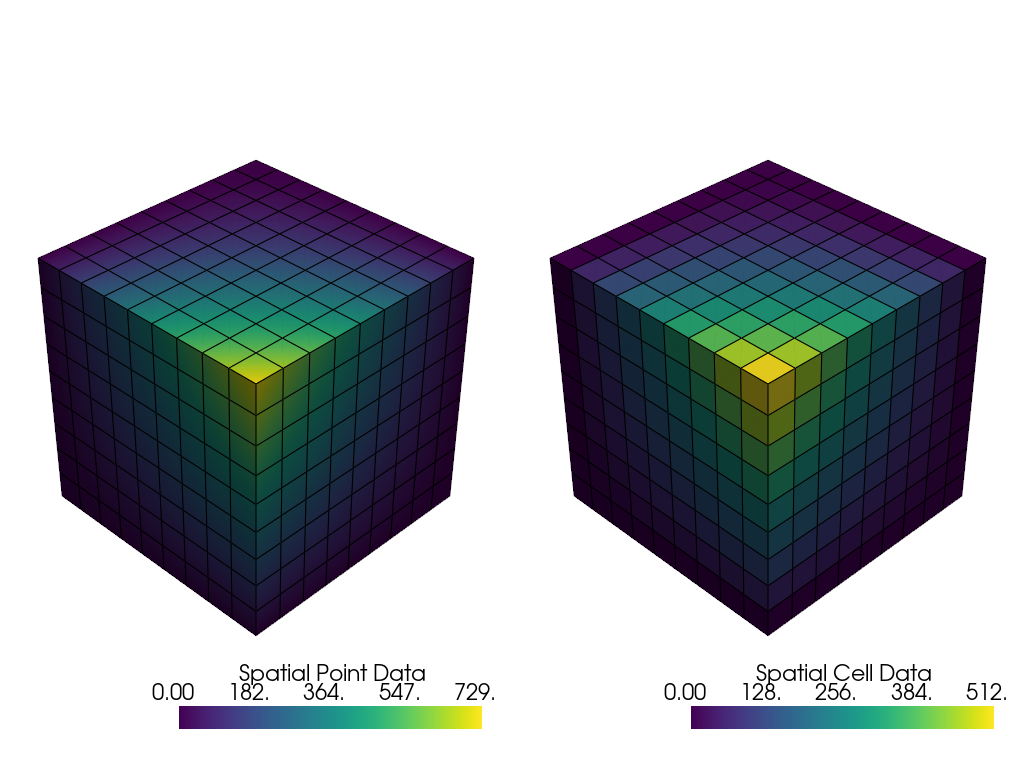
Here’s a comparison of point data versus cell data and how point data is interpolated across cells when mapping colors. This is unlike cell data which has a single value across the cell’s domain:
import pyvista as pv
from pyvista import examples
uni = examples.load_uniform()
pl = pv.Plotter(shape=(1, 2), border=False)
pl.add_mesh(uni, scalars='Spatial Point Data', show_edges=True)
pl.subplot(0, 1)
pl.add_mesh(uni, scalars='Spatial Cell Data', show_edges=True)
pl.show()
Field Data#
Field data is not directly associated with either the points or cells but still should be attached to the mesh. This may be a string array storing notes, or even indices of a Collision.
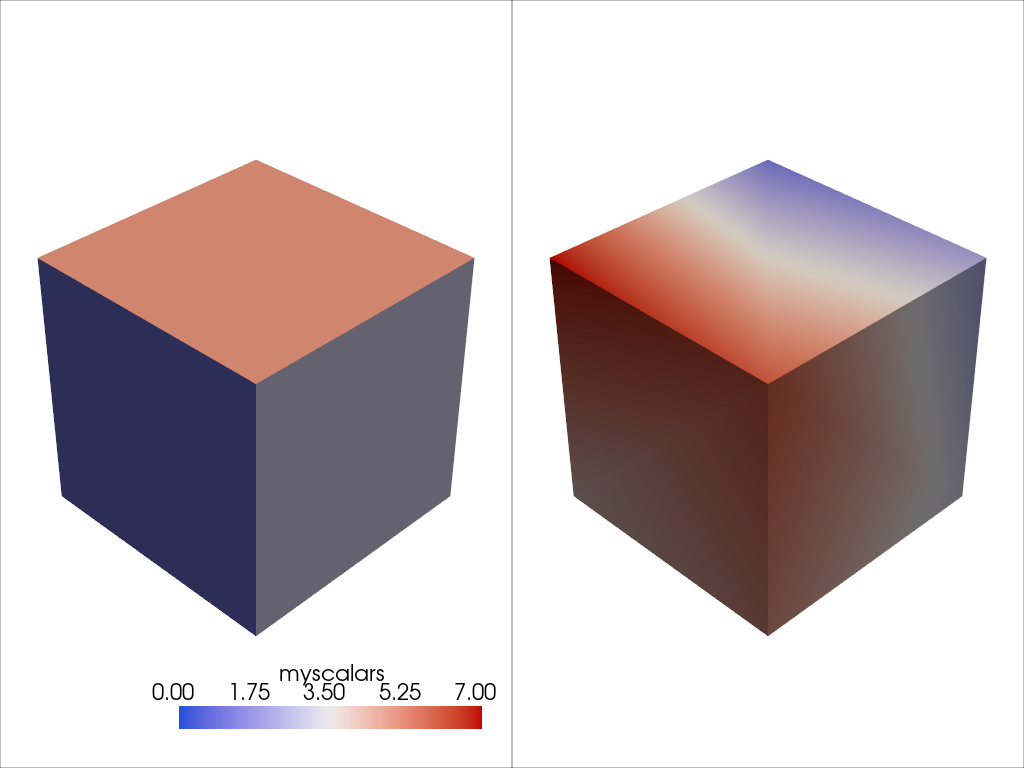
Assigning Scalars to a Mesh#
Here’s how we assign values to cell attributes and plot it. Here, we
generate cube containing 6 faces and assign each face an integer from
range(6) and then have it plotted.
Note how this varies from assigning scalars to each point
cube = pv.Cube()
cube.cell_data['myscalars'] = range(6)
other_cube = cube.copy()
other_cube.point_data['myscalars'] = range(8)
pl = pv.Plotter(shape=(1, 2), border_width=1)
pl.add_mesh(cube, cmap='coolwarm')
pl.subplot(0, 1)
pl.add_mesh(other_cube, cmap='coolwarm')
pl.show()