pyvista.DataSetFilters.compute_implicit_distance#
- DataSetFilters.compute_implicit_distance( )[source]#
Compute the implicit distance from the points to a surface.
This filter will compute the implicit distance from all of the nodes of this mesh to a given surface. This distance will be added as a point array called
'implicit_distance'.Nodes of this mesh which are interior to the input surface geometry have a negative distance, and nodes on the exterior have a positive distance. Nodes which intersect the input surface has a distance of zero.
- Parameters:
- surface
pyvista.DataSet The surface used to compute the distance.
- inplacebool, default:
False If
True, a new scalar array will be added to thepoint_dataof this mesh and the modified mesh will be returned. Otherwise a copy of this mesh is returned with that scalar field added.
- surface
- Returns:
pyvista.DataSetDataset containing the
'implicit_distance'array inpoint_data.
Examples
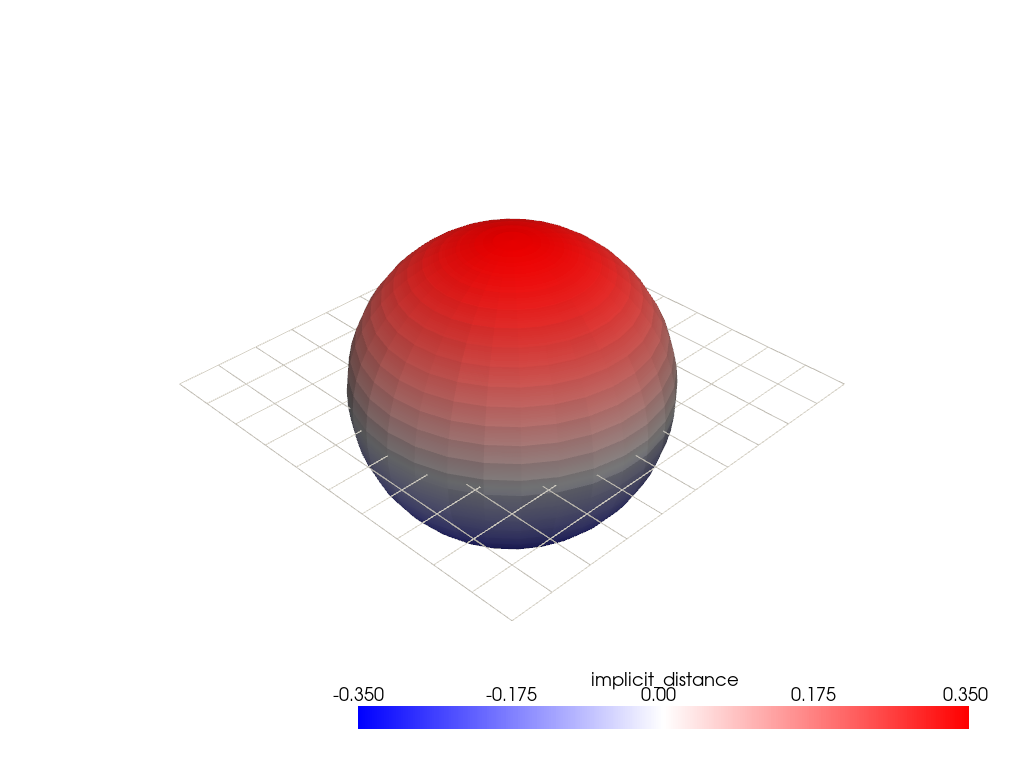
Compute the distance between all the points on a sphere and a plane.
>>> import pyvista as pv >>> sphere = pv.Sphere(radius=0.35) >>> plane = pv.Plane() >>> _ = sphere.compute_implicit_distance(plane, inplace=True) >>> dist = sphere['implicit_distance'] >>> type(dist) <class 'pyvista.core.pyvista_ndarray.pyvista_ndarray'>
Plot these distances as a heatmap. Note how distances above the plane are positive, and distances below the plane are negative.
>>> pl = pv.Plotter() >>> _ = pl.add_mesh(sphere, scalars='implicit_distance', cmap='bwr') >>> _ = pl.add_mesh(plane, color='w', style='wireframe') >>> pl.show()
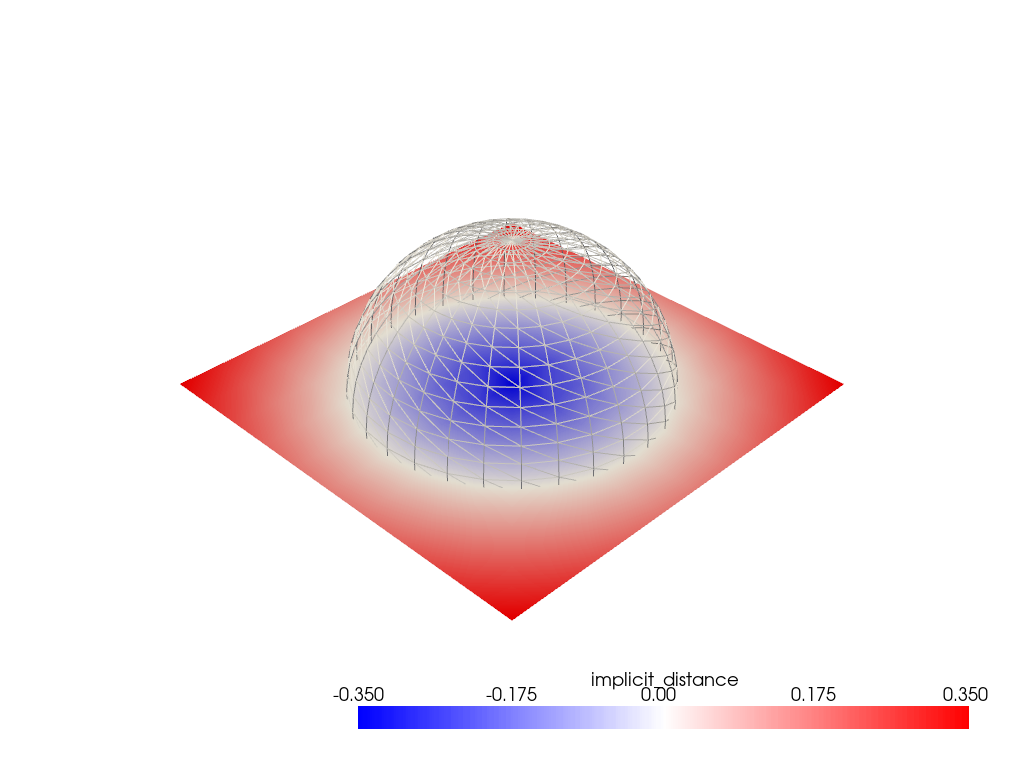
We can also compute the distance from all the points on the plane to the sphere.
>>> _ = plane.compute_implicit_distance(sphere, inplace=True)
Again, we can plot these distances as a heatmap. Note how distances inside the sphere are negative and distances outside the sphere are positive.
>>> pl = pv.Plotter() >>> _ = pl.add_mesh( ... plane, ... scalars='implicit_distance', ... cmap='bwr', ... clim=[-0.35, 0.35], ... ) >>> _ = pl.add_mesh(sphere, color='w', style='wireframe') >>> pl.show()
See Clipping with a Surface and Voxelize a Surface Mesh for more examples using this filter.