pyvista.ImageData.to_tetrahedra#
- ImageData.to_tetrahedra(
- tetra_per_cell: int = 5,
- mixed: str | Sequence[int] | bool = False,
- pass_cell_ids: bool = True,
- pass_data: bool = True,
- progress_bar: bool = False,
Create a tetrahedral mesh structured grid.
- Parameters:
- tetra_per_cell
int, default: 5 The number of tetrahedrons to divide each cell into. Can be either
5,6, or12. Ifmixed=True, this value is overridden.- mixed
str, bool, sequence, default:False When set, subdivides some cells into 5 and some cells into 12. Set to
Trueto use the active cell scalars of thepyvista.RectilinearGridto be either 5 or 12 to determining the number of tetrahedra to generate per cell.When a sequence, uses these values to subdivide the cells. When a string uses a cell array rather than the active array to determine the number of tetrahedra to generate per cell.
- pass_cell_idsbool, default:
True Set to
Trueto make the tetrahedra have scalar data indicating which cell they came from in the originalpyvista.RectilinearGrid. The name of this array is'vtkOriginalCellIds'within thecell_data.- pass_databool, default:
True Set to
Trueto make the tetrahedra mesh have the cell data from the originalpyvista.RectilinearGrid. This usespass_cell_ids=Trueinternally. IfTrue,pass_cell_idswill also be set toTrue.- progress_barbool, default:
False Display a progress bar to indicate progress.
- tetra_per_cell
- Returns:
pyvista.UnstructuredGridUnstructuredGrid containing the tetrahedral cells.
Examples
Divide a rectangular grid into tetrahedrons. Each cell contains by default 5 tetrahedrons.
First, create and plot the grid.
>>> import numpy as np >>> import pyvista as pv >>> xrng = np.linspace(0, 1, 2) >>> yrng = np.linspace(0, 1, 2) >>> zrng = np.linspace(0, 2, 3) >>> grid = pv.RectilinearGrid(xrng, yrng, zrng) >>> grid.plot()

Now, generate the tetrahedra plot in the exploded view of the cell.
>>> tet_grid = grid.to_tetrahedra() >>> tet_grid.explode(factor=0.5).plot(show_edges=True)

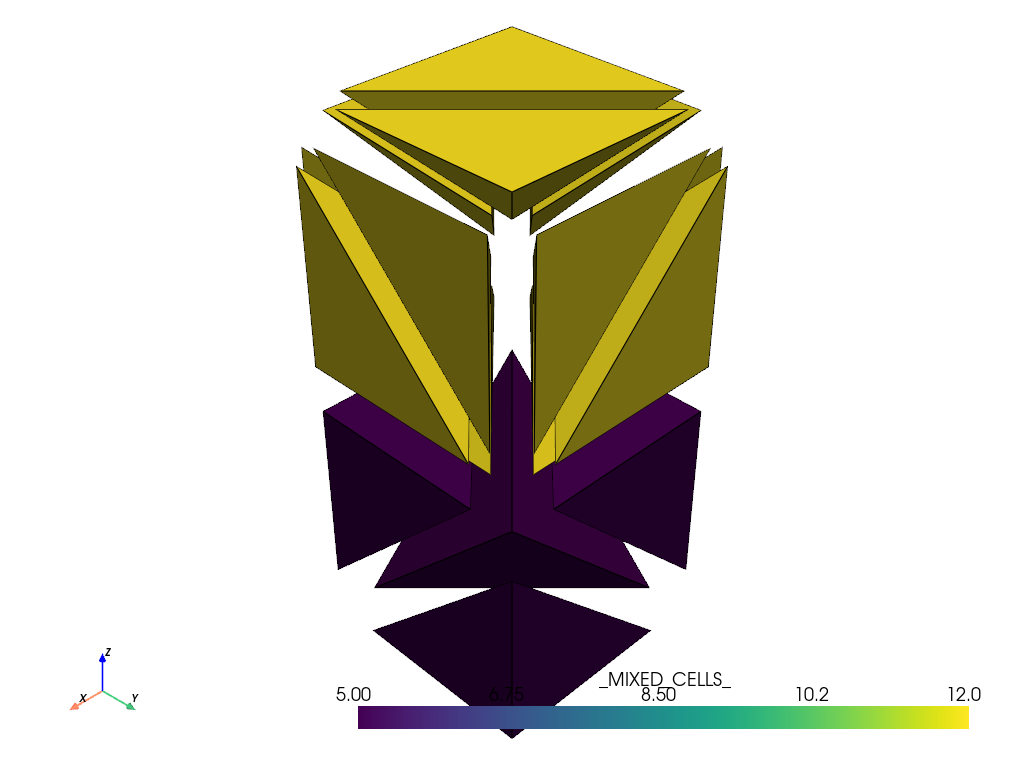
Take the same grid but divide the first cell into 5 cells and the other cell into 12 tetrahedrons per cell.
>>> tet_grid = grid.to_tetrahedra(mixed=[5, 12]) >>> tet_grid.explode(factor=0.5).plot(show_edges=True)