pyvista.PolyDataFilters.boolean_intersection#
- PolyDataFilters.boolean_intersection(
- other_mesh,
- tolerance=1e-05,
- progress_bar: bool = False,
Perform a boolean intersection operation on two meshes.
Essentially, boolean union, difference, and intersection are all the same operation. Just different parts of the objects are kept at the end.
The intersection of two manifold meshes
AandBis the mesh which is the volume ofAthat is also inB.Note
If your boolean operations don’t react the way you think they should (i.e. the wrong parts disappear), one of your meshes probably has its normals pointing inward. Use
PolyDataFilters.plot_normals()to visualize the normals.Note
This method returns the “volume” intersection between two meshes whereas the
PolyDataFilters.intersection()filter returns the surface intersection between two meshes (which often resolves as a line).Note
Both meshes must be composed of all triangles. Check with
PolyData.is_all_trianglesand convert withPolyDataFilters.triangulate().Added in version 0.32.0.
Changed in version 0.45.0: Define
&operator to perform boolean intersection.- Parameters:
- other_mesh
pyvista.PolyData Mesh operating on the source mesh.
- tolerance
float, default: 1e-5 Tolerance used to determine when a point’s absolute distance is considered to be zero.
- progress_barbool, default:
False Display a progress bar to indicate progress.
- other_mesh
- Returns:
pyvista.PolyDataThe result of the boolean operation.
Examples
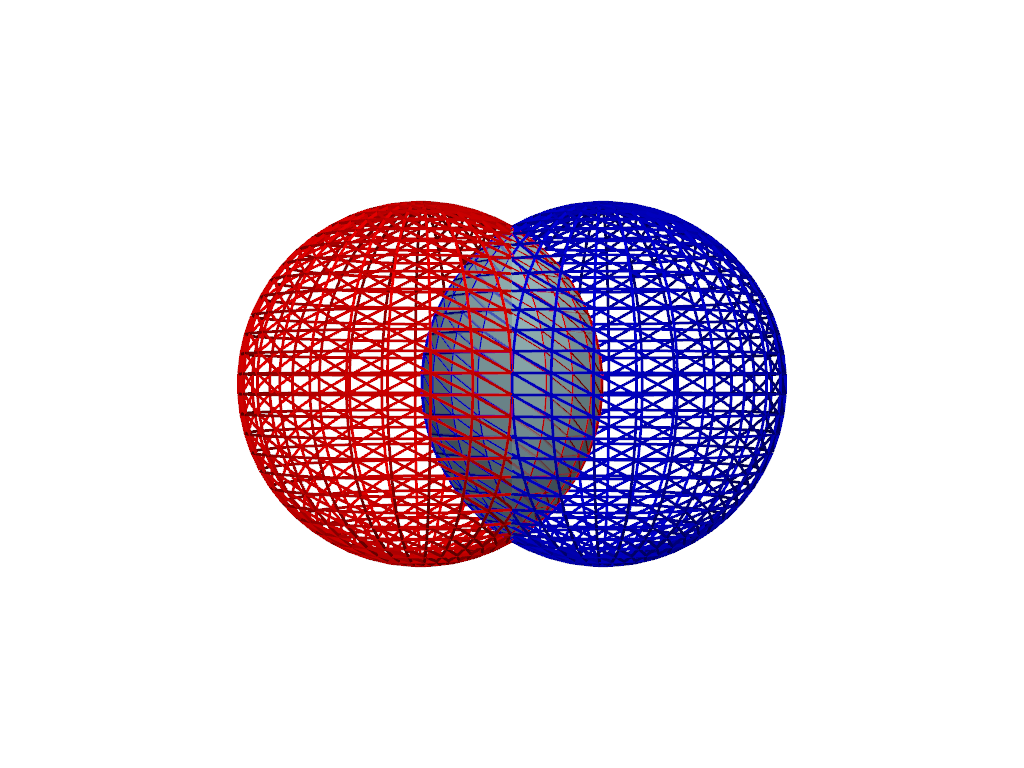
Demonstrate a boolean intersection with two spheres. Note how the final mesh only includes the intersection of the two.
>>> import pyvista as pv >>> sphere_a = pv.Sphere() >>> sphere_b = pv.Sphere(center=(0.5, 0, 0)) >>> result = sphere_a & sphere_b >>> pl = pv.Plotter() >>> _ = pl.add_mesh(sphere_a, color='r', style='wireframe', line_width=3) >>> _ = pl.add_mesh(sphere_b, color='b', style='wireframe', line_width=3) >>> _ = pl.add_mesh(result, color='lightblue') >>> pl.camera_position = 'xz' >>> pl.show()
See Boolean Operations for more examples using this filter.