Transitioning from VTK to PyVista

VTK is primarily developed in C++ and uses chained setter and getter commands to access data. Instead, PyVista wraps the VTK data types into numpy arrays so that users can benefit from its bracket syntax and fancy indexing. This section demonstrates the difference between the two approaches in a series of examples.

For example, to hard-code points for a vtk.vtkImageData data structure using VTK Python’s bindings, one would write the following:

>>> import vtk
>>> from math import cos, sin

Create (x, y) points for a 300x300 image dataset

>>> points = vtk.vtkDoubleArray()
>>> points.SetName("points")
>>> points.SetNumberOfComponents(1)
>>> points.SetNumberOfTuples(300*300)

>>> for x in range(300):
...     for y in range(300):
...         points.SetValue(x*300 + y, 127.5 + (1.0 + sin(x/25.0)*cos(y/25.0)))

Create the image structure

>>> image_data = vtk.vtkImageData()
>>> image_data.SetOrigin(0, 0, 0)
>>> image_data.SetSpacing(1, 1, 1)
>>> image_data.SetDimensions(300, 300, 1)

Assign the points to the image

>>> image_data.GetPointData().SetScalars(points)

As you can see, there is quite a bit of boilerplate that goes into the creation of a simple vtk.vtkImageData dataset. PyVista provides much more concise syntax that is more “Pythonic.” The equivalent code in PyVista is:

>>> import pyvista
>>> import numpy as np

Use the meshgrid function to create 2D "grids" of the x and y values.
This section effectively replaces the vtkDoubleArray.

>>> xi = np.arange(300)
>>> x, y = np.meshgrid(xi, xi)
>>> values = 127.5 + (1.0 + np.sin(x/25.0)*np.cos(y/25.0))

Create the grid. Note how the values must use Fortran ordering.

>>> grid = pyvista.ImageData(dimensions=(300, 300, 1))
>>> grid.point_data["values"] = values.flatten(order="F")

Here, PyVista has done several things for us:

1. PyVista combines the dimensionality of the data (in the shape of the numpy.ndarray) with the values of the data in one line. VTK uses “tuples” to describe the shape of the data (where it sits in space) and “components” to describe the type of data (1 = scalars/scalar fields, 2 = vectors/vector fields, n = tensors/tensor fields). Here, shape and values are stored concretely in one variable.

2. pyvista.ImageData wraps vtk.vtkImageData, just with a different name; they are both containers of evenly spaced points. Your data does not have to be an “image” to use it with vtk.vtkImageData; rather, like images, values in the dataset are evenly spaced apart like pixels in an image.

   Furthermore, since we know the container is for uniformly spaced data, pyvista sets the origin and spacing by default to (0, 0, 0) and (1, 1, 1). This is another great thing about PyVista and Python. Rather than having to know everything about the VTK library up front, you can get started very easily. Once you get more familiar with it and need to do something more complex, you can dive deeper. For example, changing the origin and spacing is as simple as:

   >>> grid.origin = (10, 20, 10)
   >>> grid.spacing = (2, 3, 5)
   

3. The name for the point_array is given directly in dictionary-style fashion. Also, since VTK stores data on the heap (linear segments of RAM; a C++ concept), the data must be flattened and put in Fortran ordering (which controls how multidimensional data is laid out in physically 1D memory; numpy uses “C”-style memory layout by default). This is why in our earlier example, the first argument to SetValue() was written as x*300 + y. Here, numpy takes care of this for us quite nicely and it’s made more explicit in the code, following the Python best practice of “Explicit is better than implicit.”

Finally, with PyVista, each geometry class contains methods that allow you to immediately plot the mesh without also setting up the plot. For example, in VTK you would have to do:

>>> actor = vtk.vtkImageActor()
>>> actor.GetMapper().SetInputData(image_data)
>>> ren = vtk.vtkRenderer()
>>> renWin = vtk.vtkRenderWindow()
>>> renWin.AddRenderer(ren)
>>> renWin.SetWindowName('ReadSTL')
>>> iren = vtk.vtkRenderWindowInteractor()
>>> iren.SetRenderWindow(renWin)
>>> ren.AddActor(actor)
>>> iren.Initialize()
>>> renWin.Render()
>>> iren.Start()

However, with PyVista you only need:

grid.plot(cpos='xy', show_scalar_bar=False, cmap='coolwarm')

Static Scene

Interactive Scene

PointSet Construction

PyVista heavily relies on NumPy to efficiently allocate and access VTK’s C arrays. For example, to create an array of points within VTK one would normally loop through all the points of a list and supply that to a vtkPoints class. For example:

>>> import vtk
>>> vtk_array = vtk.vtkDoubleArray()
>>> vtk_array.SetNumberOfComponents(3)
>>> vtk_array.SetNumberOfValues(9)
>>> vtk_array.SetValue(0, 0)
>>> vtk_array.SetValue(1, 0)
>>> vtk_array.SetValue(2, 0)
>>> vtk_array.SetValue(3, 1)
>>> vtk_array.SetValue(4, 0)
>>> vtk_array.SetValue(5, 0)
>>> vtk_array.SetValue(6, 0.5)
>>> vtk_array.SetValue(7, 0.667)
>>> vtk_array.SetValue(8, 0)
>>> vtk_points = vtk.vtkPoints()
>>> vtk_points.SetData(vtk_array)
>>> print(vtk_points)

vtkPoints (0x5606a643dee0)
  Debug: Off
  Modified Time: 90
  Reference Count: 1
  Registered Events: (none)
  Data: 0x5606a643d140
  Data Array Name: Points
  Number Of Points: 3
  Bounds: 
    Xmin,Xmax: (0, 1)
    Ymin,Ymax: (0, 0.667)
    Zmin,Zmax: (0, 0)

To do the same within PyVista, you simply need to create a NumPy array:

>>> import numpy as np
>>> np_points = np.array([[0, 0, 0],
...                       [1, 0, 0],
...                       [0.5, 0.667, 0]])

Note

You can use pyvista.vtk_points() to construct a vtkPoints object, but this is unnecessary in almost all situations.

Since the end goal is to construct a pyvista.DataSet, you would simply pass the np_points array to the pyvista.PolyData constructor:

>>> import pyvista
>>> poly_data = pyvista.PolyData(np_points)

Whereas in VTK you would have to do:

>>> vtk_poly_data = vtk.vtkPolyData()
>>> vtk_poly_data.SetPoints(vtk_points)

The same goes with assigning face or cell connectivity/topology. With VTK you would normally have to loop using InsertNextCell and InsertCellPoint. For example, to create a single cell (triangle) and then assign it to vtkPolyData:

>>> cell_arr = vtk.vtkCellArray()
>>> cell_arr.InsertNextCell(3)
>>> cell_arr.InsertCellPoint(0)
>>> cell_arr.InsertCellPoint(1)
>>> cell_arr.InsertCellPoint(2)
>>> vtk_poly_data.SetPolys(cell_arr)

In PyVista, we can assign this directly in the constructor and then access it (or change it) from the faces attribute.

>>> faces = np.array([3, 0, 1, 2])
>>> poly_data = pyvista.PolyData(np_points, faces)
>>> poly_data.faces

array([3, 0, 1, 2])

Object Representation

Both VTK and PyVista provide representations for their objects.

VTK provides a verbose representation (useful for debugging) of their data types that can be accessed via print(), as the __repr__ (unlike __str__) only provides minimal information about each object:

>>> print(vtk_poly_data)

vtkPolyData (0x5606a67875a0)
  Debug: Off
  Modified Time: 161
  Reference Count: 1
  Registered Events: (none)
  Information: 0x5606a6cfabe0
  Data Released: False
  Global Release Data: Off
  UpdateTime: 0
  Field Data:
    Debug: Off
    Modified Time: 142
    Reference Count: 1
    Registered Events: (none)
    Number Of Arrays: 0
    Number Of Components: 0
    Number Of Tuples: 0
  Number Of Points: 3
  Number Of Cells: 1
  Cell Data:
    Debug: Off
    Modified Time: 145
    Reference Count: 1
    Registered Events: 
      Registered Observers:
        vtkObserver (0x5606a6e35f70)
          Event: 33
          EventName: ModifiedEvent
          Command: 0x5606a6ce0360
          Priority: 0
          Tag: 1
    Number Of Arrays: 0
    Number Of Components: 0
    Number Of Tuples: 0
    Copy Tuple Flags: ( 1 1 1 1 1 0 1 1 1 1 1 1 )
    Interpolate Flags: ( 1 1 1 1 1 0 0 1 1 1 1 0 )
    Pass Through Flags: ( 1 1 1 1 1 1 1 1 1 1 1 1 )
    Scalars: (none)
    Vectors: (none)
    Normals: (none)
    TCoords: (none)
    Tensors: (none)
    GlobalIds: (none)
    PedigreeIds: (none)
    EdgeFlag: (none)
    Tangents: (none)
    RationalWeights: (none)
    HigherOrderDegrees: (none)
    ProcessIds: (none)
  Point Data:
    Debug: Off
    Modified Time: 144
    Reference Count: 1
    Registered Events: 
      Registered Observers:
        vtkObserver (0x5606a6e226b0)
          Event: 33
          EventName: ModifiedEvent
          Command: 0x5606a6ce0360
          Priority: 0
          Tag: 1
    Number Of Arrays: 0
    Number Of Components: 0
    Number Of Tuples: 0
    Copy Tuple Flags: ( 1 1 1 1 1 0 1 1 1 1 1 1 )
    Interpolate Flags: ( 1 1 1 1 1 0 0 1 1 1 1 0 )
    Pass Through Flags: ( 1 1 1 1 1 1 1 1 1 1 1 1 )
    Scalars: (none)
    Vectors: (none)
    Normals: (none)
    TCoords: (none)
    Tensors: (none)
    GlobalIds: (none)
    PedigreeIds: (none)
    EdgeFlag: (none)
    Tangents: (none)
    RationalWeights: (none)
    HigherOrderDegrees: (none)
    ProcessIds: (none)
  Bounds: 
    Xmin,Xmax: (0, 1)
    Ymin,Ymax: (0, 0.667)
    Zmin,Zmax: (0, 0)
  Compute Time: 213
  Editable: false
  Number Of Points: 3
  Point Coordinates: 0x5606a643dee0
  PointLocator: 0
  CellLocator: 0
  Number Of Vertices: 0
  Number Of Lines: 0
  Number Of Polygons: 1
  Number Of Triangle Strips: 0
  Number Of Pieces: 1
  Piece: -1
  Ghost Level: 0
  CellsBounds: 
    Xmin,Xmax: (0, 1)
    Ymin,Ymax: (0, 0.667)
    Zmin,Zmax: (0, 0)
  CellsBounds Time: 214

PyVista chooses to show minimal data in the repr(), preferring explicit attribute access on meshes for the bulk of attributes. For example:

>>> poly_data

PolyData	Information
N Cells	1
N Points	3
N Strips	0
X Bounds	0.000e+00, 1.000e+00
Y Bounds	0.000e+00, 6.670e-01
Z Bounds	0.000e+00, 0.000e+00
N Arrays	0

In this representation we see:

• Number of cells n_cells

• Number of points n_points

• Bounds of the mesh bounds

• Number of data arrays n_arrays

All other attributes like lines, point_data, or cell_data can be accessed directly from the object. This approach was chosen to allow for a brief summary showing key parts of the DataSet without overwhelming the user.

Tradeoffs

While most features can, not everything can be simplified without losing functionality or performance.

In the collision filter, we demonstrate how to calculate the collision between two meshes. For example:

import pyvista

# create a default sphere and a shifted sphere
mesh_a = pyvista.Sphere()
mesh_b = pyvista.Sphere(center=(-0.4, 0, 0))
out, n_coll = mesh_a.collision(mesh_b, generate_scalars=True, contact_mode=2)

pl = pyvista.Plotter()
pl.add_mesh(out)
pl.add_mesh(mesh_b, style='wireframe', color='k')
pl.camera_position = 'xy'
pl.show()

Static Scene

Interactive Scene

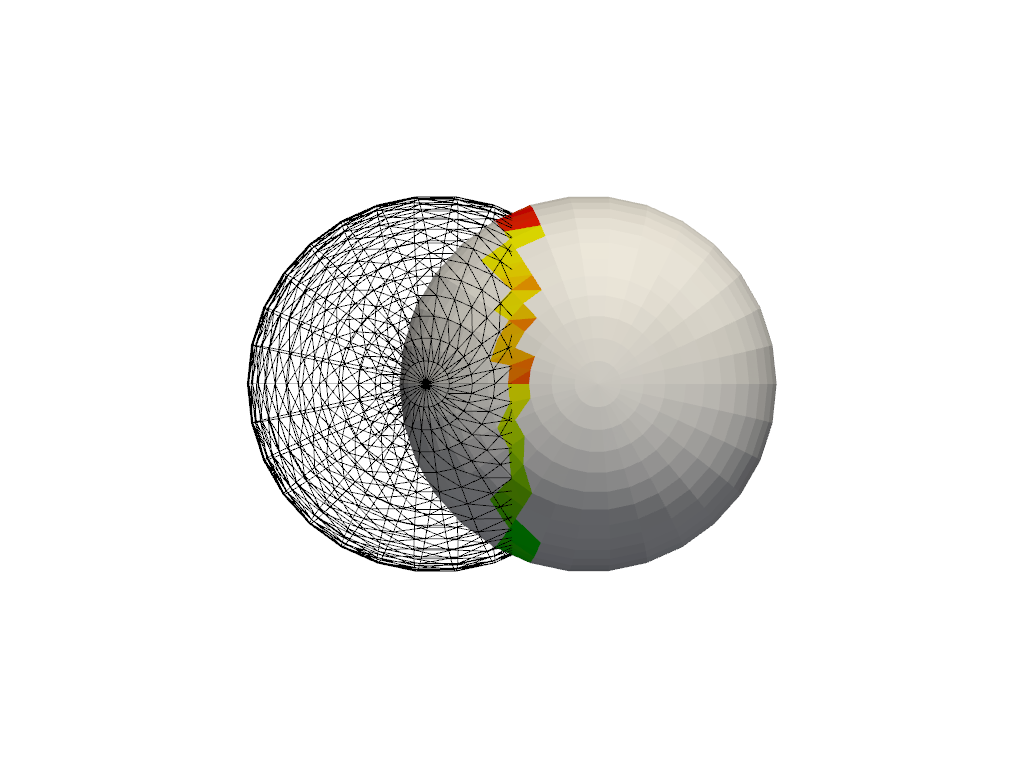
Under the hood, the collision filter detects mesh collisions using oriented bounding box (OBB) trees. For a single collision, this filter is as performant as the VTK counterpart, but when computing multiple collisions with the same meshes, as in the Collision example, it is more efficient to use the vtkCollisionDetectionFilter, as the OBB tree is computed once for each mesh. In most cases, pure PyVista is sufficient for most data science, but there are times when you may want to use VTK classes directly.

Note that nothing stops you from using VTK classes and then wrapping the output with PyVista. For example:

import vtk
import pyvista

# Create a circle using vtk
polygonSource = vtk.vtkRegularPolygonSource()
polygonSource.GeneratePolygonOff()
polygonSource.SetNumberOfSides(50)
polygonSource.SetRadius(5.0)
polygonSource.SetCenter(0.0, 0.0, 0.0)
polygonSource.Update()

# wrap and plot using pyvista
mesh = pyvista.wrap(polygonSource.GetOutput())
mesh.plot(line_width=3, cpos='xy', color='k')

Static Scene

Interactive Scene

In this manner, you can get the “best of both worlds” should you need the flexibility of PyVista and the raw power of VTK.

Note

You can use pyvista.Polygon() for a one line replacement of the above VTK code.