Note
Go to the end to download the full example code.
Mesh Validation#
This example explores different cases where a mesh may not be considered valid as defined
by the validate_mesh() method.
from __future__ import annotations
import pyvista as pv
from pyvista.examples import plot_cell
Non-convex cells#
Many VTK algorithms assume that cells are convex. This can result in incorrect outputs
and may also affect rendering. For example, let’s create PolyData
with a concave QUAD cell.
Use validate_mesh() to show that the cell is not
convex.
report = quad.validate_mesh()
assert not report.is_valid
assert report.invalid_fields == ('non_convex',)
If we plot the cell, we can see that the concave cell is incorrectly rendered as though it’s convex even though it is not.
plot_cell(quad, 'xy')
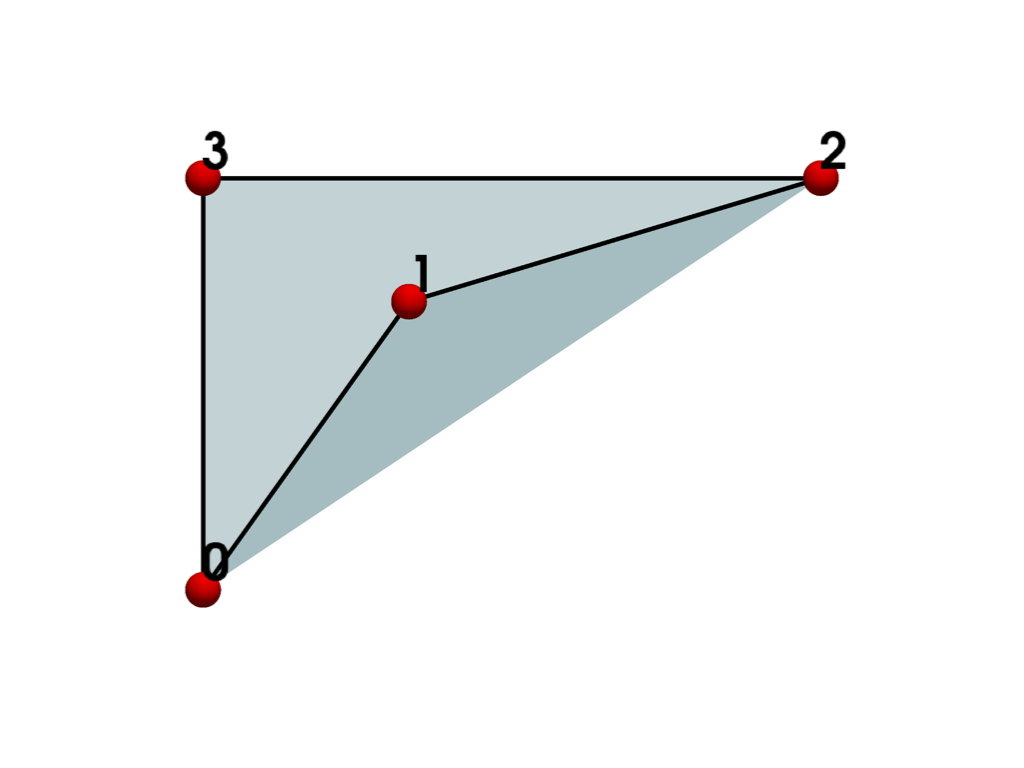
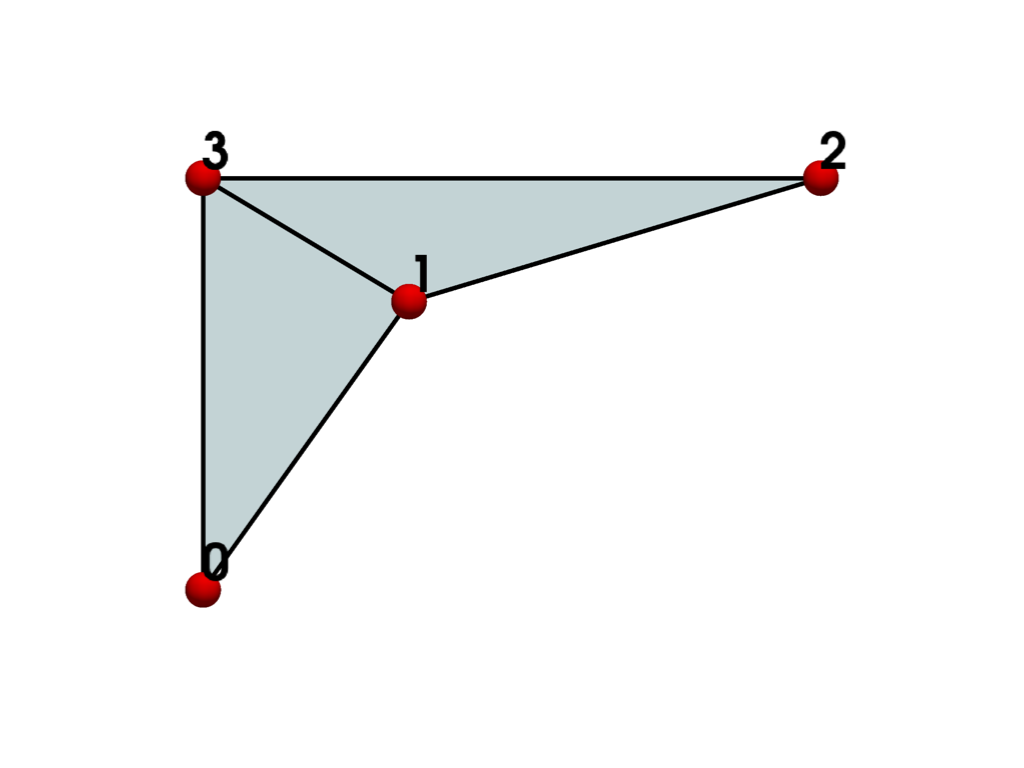
To address the convexity problem, we can triangulate()
the mesh. The mesh is now valid and renders correctly.
triangles = quad.triangulate()
report = triangles.validate_mesh()
assert report.is_valid
plot_cell(triangles, 'xy')
Cells with inverted faces#
Cells with inverted faces can result in incorrect geometric computations such as
cell volume or centroid. To demonstrate this, we first create a valid
POLYHEDRON cell similar to the
Polyhedron() example cell.
points = [[0, 0, 0], [1, 0, 0], [0.5, 0.5, 0], [0, 0, 1]]
cells = [4, 3, 0, 2, 1, 3, 0, 1, 3, 3, 0, 3, 2, 3, 1, 2, 3]
cells = [len(cells), *cells.copy()]
polyhedron = pv.UnstructuredGrid(cells, [pv.CellType.POLYHEDRON], points)
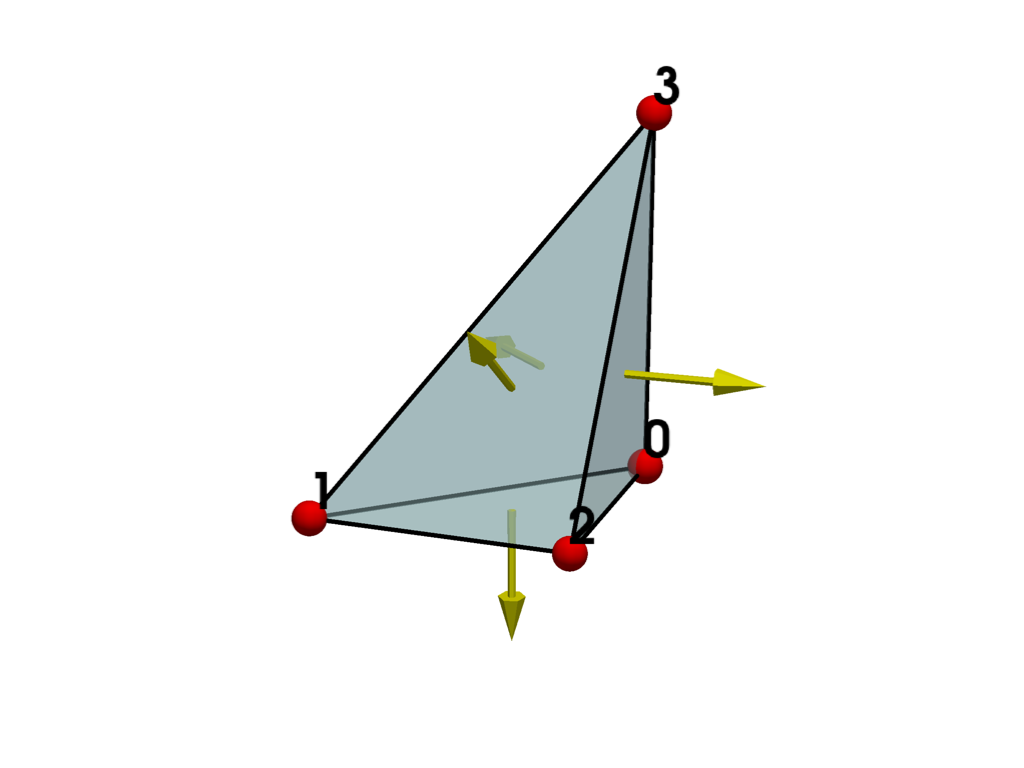
Plot the cell and show its normals. Since all points have counter-clockwise traversal, the normals all point outward and the cell is valid.
report = polyhedron.validate_mesh()
assert report.is_valid
plot_cell(polyhedron, show_normals=True)
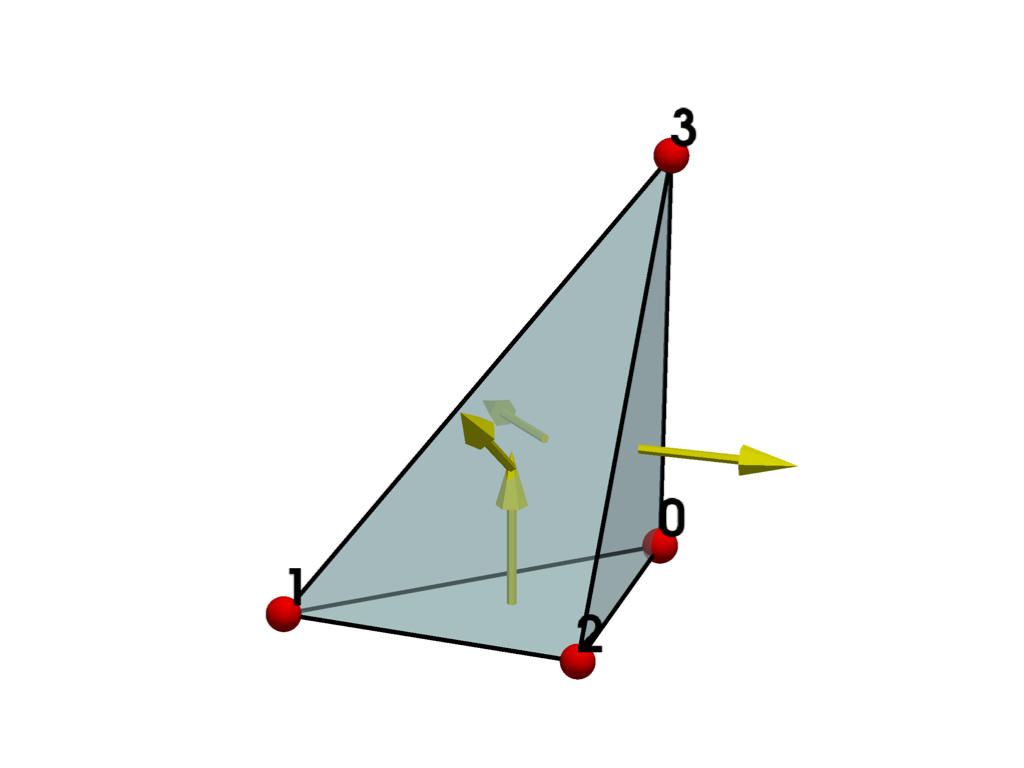
Now swap two points in the polyhedron’s connectivity to generate an otherwise identical polyhedron with a single incorrectly oriented face.
The cell is now invalid, and the bottom face is incorrectly oriented with its normal pointing inward.
report = invalid_polyhedron.validate_mesh()
assert not report.is_valid
assert report.invalid_fields == ('inverted_faces',)
plot_cell(invalid_polyhedron, show_normals=True)
Now let’s compare the centroid of the valid and invalid cells using
cell_centers(). The computed centroids differ,
demonstrating the need to have valid cells when using filters that depend on geometric
properties.
valid_centroid = polyhedron.cell_centers().points[0].tolist()
print(valid_centroid)
invalid_centroid = invalid_polyhedron.cell_centers().points[0].tolist()
print(invalid_centroid)
assert valid_centroid != invalid_centroid
[0.37499999999999994, 0.12499999999999997, 0.24999999999999994]
[0.28125000000000006, 0.09375, 0.43749999999999994]
Self-intersecting cells#
Most cell types have a defined point order which must
be respected. For example, let’s try to create a HEXAHEDRON
cell with eight points:
points = [
[0.0, 0.0, 0.0],
[1.0, 0.0, 0.0],
[0.0, 1.0, 0.0],
[0.0, 0.0, 1.0],
[1.0, 1.0, 0.0],
[1.0, 0.0, 1.0],
[0.0, 1.0, 1.0],
[1.0, 1.0, 1.0],
]
cells = [8, 0, 1, 2, 3, 4, 5, 6, 7]
celltype = [pv.CellType.HEXAHEDRON]
hexahedron = pv.UnstructuredGrid(cells, celltype, points)
At a quick glance, the cell may appear to be valid, but it is not, since the point ordering is incorrect.
report = hexahedron.validate_mesh()
assert not report.is_valid
plot_cell(hexahedron)
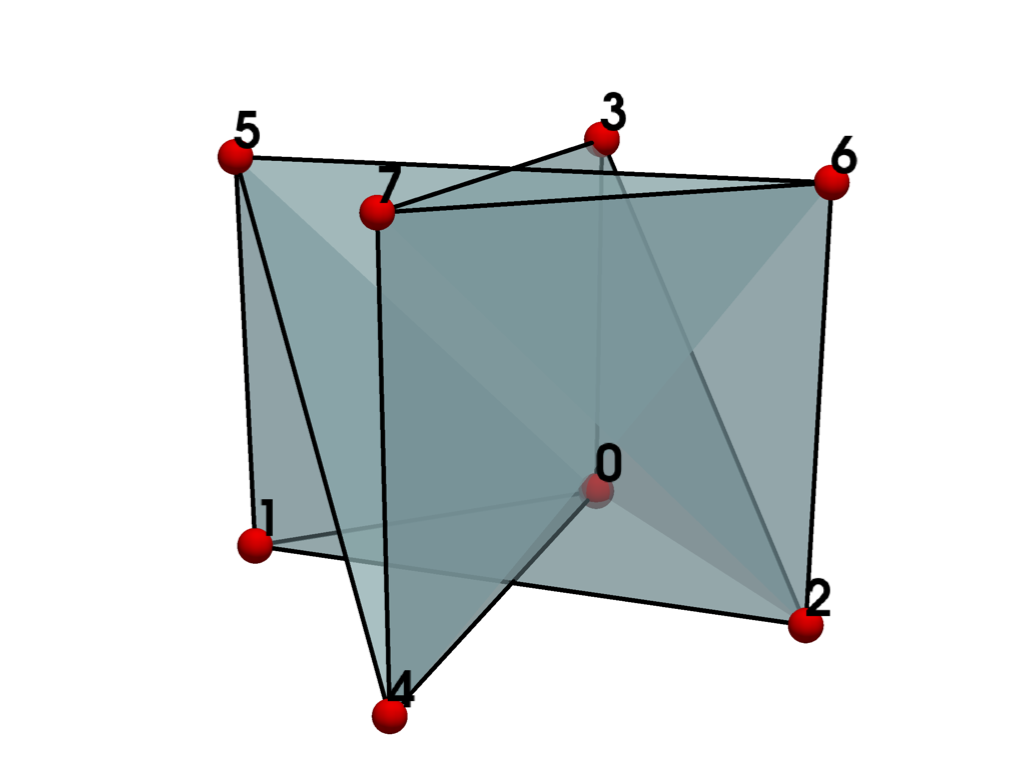
Let’s review the invalid fields reported.
assert report.invalid_fields == (
'intersecting_edges',
'inverted_faces',
'non_planar_faces',
)
From the plot above, we can visually confirm these issues since some faces appear to
intersect, and others appear to be “folded” and hence there are non-planar. To
investigate the 'inverted_faces' problem further, let’s plot the cell again with
normals.
plot_cell(hexahedron, show_normals=True)
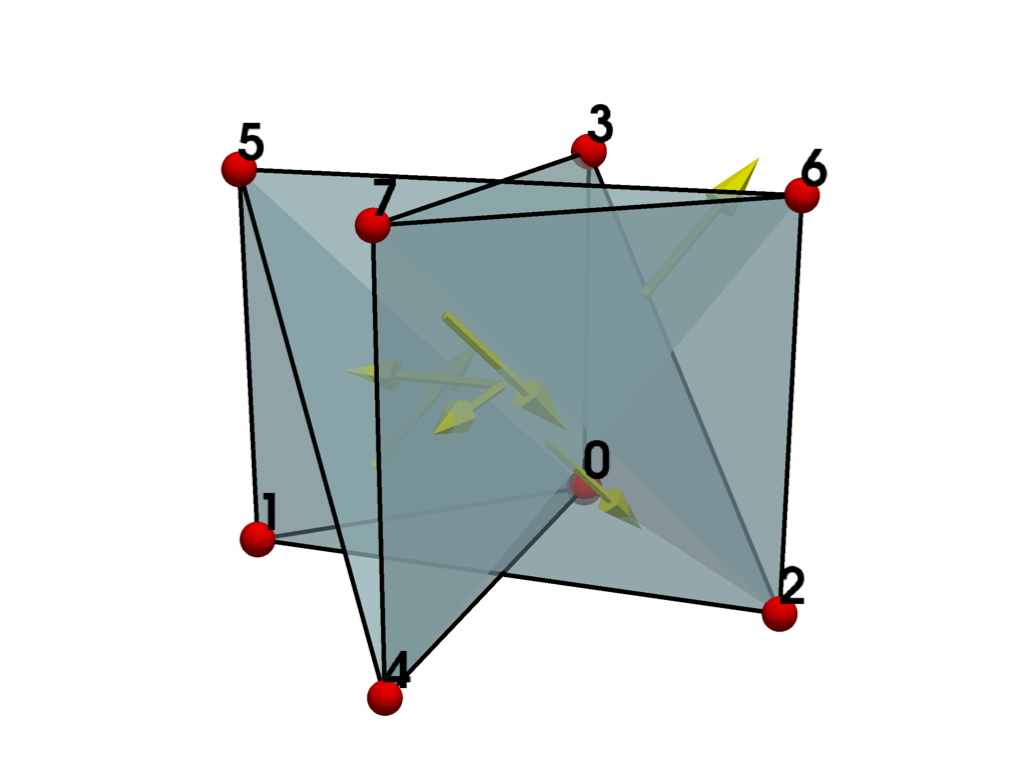
Since some of the normals are pointing inward, this confirms that there are inverted faces. To make the cell valid, we need to re-order the cell connectivity based on the required ordering stated in the documentation for vtkHexahedron.
cells = [8, 0, 1, 4, 2, 3, 5, 7, 6] # instead of [8, 0, 1, 2, 3, 4, 5, 6, 7]
celltype = [pv.CellType.HEXAHEDRON]
hexahedron = pv.UnstructuredGrid(cells, celltype, points)
report = hexahedron.validate_mesh()
assert report.is_valid
plot_cell(hexahedron)
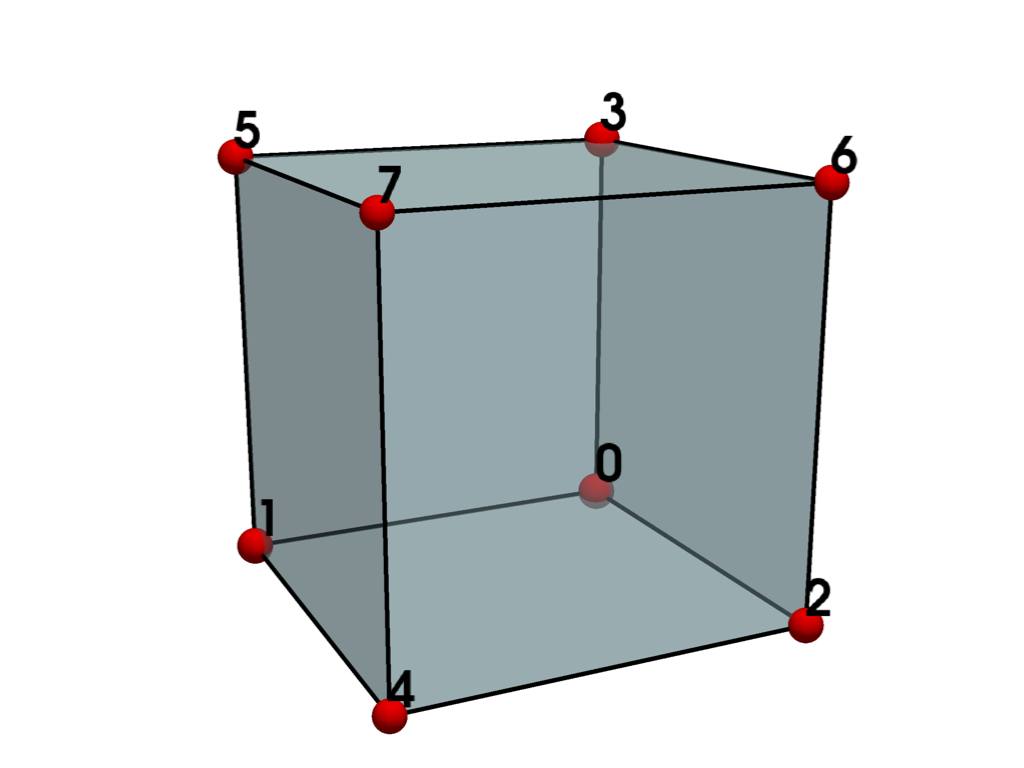
Meshes with unused points#
Unused points are points not associated with any cells. These points are not processed
consistently by filters and are often ignored or removed. To demonstrate this, create an
UnstructuredGrid with a single unused point.
grid = pv.UnstructuredGrid()
grid.points = [[0.0, 0.0, 0.0]]
assert grid.n_points == 1
assert grid.n_cells == 0
This mesh is not considered valid.
report = grid.validate_mesh()
assert not report.is_valid
assert report.invalid_fields == ('unused_points',)
Use extract_surface() on the grid and observe that the
unused point is removed.
poly = grid.extract_surface(algorithm=None)
assert poly.n_points == 0
assert poly.n_cells == 0
To remedy this, it is recommended to always associate individual points with a
VERTEX cell. E.g.:
points = [[0.0, 0.0, 0.0]]
cells = [1, 0]
celltypes = [pv.CellType.VERTEX]
grid = pv.UnstructuredGrid(cells, celltypes, points)
assert grid.n_points == 1
assert grid.n_cells == 1
This time, the point is properly processed by the filter and is retained.
poly = grid.extract_surface(algorithm=None)
assert poly.n_points == 1
assert poly.n_cells == 1
This mesh is also now considered valid.
report = grid.validate_mesh()
assert report.is_valid
assert not report.invalid_fields
Total running time of the script: (0 minutes 0.944 seconds)