Extract Surface

You can extract the surface of nearly any object within pyvista using the extract_surface() filter.

from __future__ import annotations

import numpy as np
import pyvista as pv
from pyvista import CellType

Surface extraction of nonlinear cells

Here we create a single QUADRATIC_HEXAHEDRON cell and then extract its surface to demonstrate how to extract the surface of an UnstructuredGrid. First define points of a linear cell:

lin_pts = np.array(
    [
        [-1, -1, -1],  # point 0
        [1, -1, -1],  # point 1
        [1, 1, -1],  # point 2
        [-1, 1, -1],  # point 3
        [-1, -1, 1],  # point 4
        [1, -1, 1],  # point 5
        [1, 1, 1],  # point 6
        [-1, 1, 1],  # point 7
    ],
    np.double,
)

Next, define the “midside” points of a quad cell. See the definition of a vtkQuadraticHexahedron.

quad_pts = np.array(
    [
        (lin_pts[1] + lin_pts[0]) / 2,  # between point 0 and 1
        (lin_pts[1] + lin_pts[2]) / 2,  # between point 1 and 2
        (lin_pts[2] + lin_pts[3]) / 2,  # and so on...
        (lin_pts[3] + lin_pts[0]) / 2,
        (lin_pts[4] + lin_pts[5]) / 2,
        (lin_pts[5] + lin_pts[6]) / 2,
        (lin_pts[6] + lin_pts[7]) / 2,
        (lin_pts[7] + lin_pts[4]) / 2,
        (lin_pts[0] + lin_pts[4]) / 2,
        (lin_pts[1] + lin_pts[5]) / 2,
        (lin_pts[2] + lin_pts[6]) / 2,
        (lin_pts[3] + lin_pts[7]) / 2,
    ],
)

We introduce a minor variation to the location of the mid-side points seed the random numbers for reproducibility

rng = np.random.default_rng(seed=0)
quad_pts += rng.random(quad_pts.shape) * 0.3
pts = np.vstack((lin_pts, quad_pts))

Create the grid

cells = np.hstack((20, np.arange(20))).astype(np.int64, copy=False)
celltypes = np.array([CellType.QUADRATIC_HEXAHEDRON])
grid = pv.UnstructuredGrid(cells, celltypes, pts)

Finally, extract the surface and plot it. Note that the ‘dataset_surface’ algorithm is necessary to use when generating surfaces from non-linear cells. Setting algorithm=None also works.

surf = grid.extract_surface(algorithm='dataset_surface')
surf.plot(show_scalar_bar=False)

Static Scene

Interactive Scene

Nonlinear Surface Subdivision

Should your UnstructuredGrid contain quadratic cells, you can generate a smooth surface based on the position of the “mid-edge” nodes. This allows the plotting of cells containing curvature. For additional reference, please see: https://prod.sandia.gov/techlib-noauth/access-control.cgi/2004/041617.pdf

surf_subdivided = grid.extract_surface(
    algorithm='dataset_surface', nonlinear_subdivision=5
)
surf_subdivided.plot(show_scalar_bar=False)

Static Scene

Interactive Scene

Compare Surface Extraction Algorithms

The filter extract_surface() provides the option to select which internal VTK algorithm to use for surface extraction: vtkGeometryFilter or vtkDataSetSurfaceFilter. Both algorithms produce similar surfaces, but they differ in important ways. As the following examples will demonstrate, it is generally preferable to use the geometry algorithm.

Structural Preservation

The geometry algorithm preserves structure when converting between mesh types, whereas the dataset surface algorithm does not.

For example, let’s create a simple PolyData mesh using Cone() and cast it to UnstructuredGrid.

poly = pv.Cone()
ugrid = poly.cast_to_unstructured_grid()

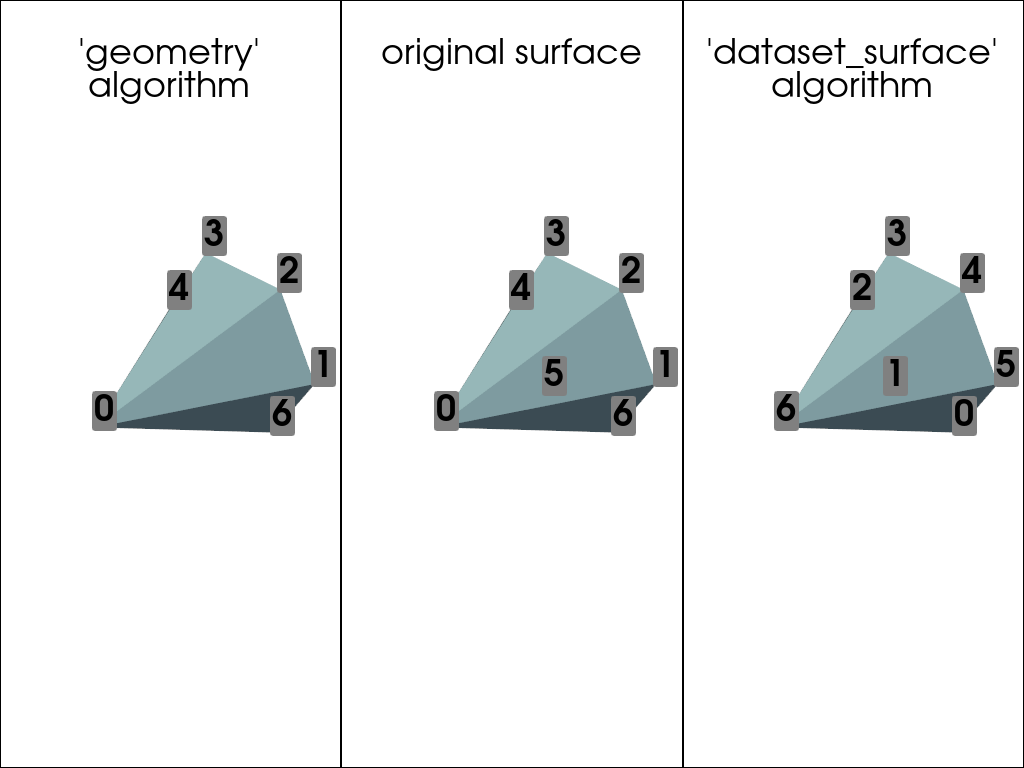
If we convert it back to a surface, the geometry algorithm returns the original surface with the same order of points and the same cell connectivity arrays.

poly_geometry = ugrid.extract_surface(
    algorithm='geometry', pass_cellid=False, pass_pointid=False
)
assert poly_geometry == poly

But the dataset surface algorithm does not.

poly_surface = ugrid.extract_surface(
    algorithm='dataset_surface', pass_cellid=False, pass_pointid=False
)
assert poly_surface != poly

Compare the point ids of the original mesh to the generated surfaces.

pl = pv.Plotter(shape=(1, 3))

pl.subplot(0, 0)
pl.add_mesh(poly_geometry)
pl.add_title("'geometry'\nalgorithm", font_size=14)
pl.add_point_labels(poly_geometry, range(poly_geometry.n_points), font_size=36)

pl.subplot(0, 1)
pl.add_mesh(poly)
pl.add_title('original surface', font_size=14)
pl.add_point_labels(poly, range(poly.n_points), font_size=36)

pl.subplot(0, 2)
pl.add_mesh(poly_surface)
pl.add_title("'dataset_surface'\nalgorithm", font_size=14)
pl.add_point_labels(poly_surface, range(poly_surface.n_points), font_size=36)

pl.link_views()
pl.show()

Static Scene

Interactive Scene

Closed Surface Generation

The geometry algorithm generates closed surfaces in cases where a closed surface is expected, whereas the dataset surface algorithm may not. For example, extract the surface of ImageData comprised of a single VOXEL cell.

grid = pv.ImageData(dimensions=(2, 2, 2))
assert grid.n_cells == 1
assert grid.distinct_cell_types == {CellType.VOXEL}
assert grid.max_cell_dimensionality == 3

Both algorithms convert the single 3D cell into a cube with six 2D QUAD faces.

poly_geometry = grid.extract_surface(algorithm='geometry')
assert poly_geometry.n_cells == 6
assert poly_geometry.distinct_cell_types == {CellType.QUAD}
assert poly_geometry.max_cell_dimensionality == 2

poly_surface = grid.extract_surface(algorithm='dataset_surface')
assert poly_surface.n_cells == 6
assert poly_surface.distinct_cell_types == {CellType.QUAD}
assert poly_geometry.max_cell_dimensionality == 2

However, the geometry algorithm returns a closed surface with eight points and no open edges.

assert poly_geometry.n_points == 8
assert poly_geometry.n_open_edges == 0

In contrast, the dataset surface algorithm returns a surface with duplicate points and many open edges.

assert poly_surface.n_points == 24
assert poly_surface.n_open_edges == 24

This can be fixed with a call to clean(), however.

cleaned = poly_surface.clean()
assert cleaned.n_points == 8
assert cleaned.n_open_edges == 0

Note that a closed surface is important for some calculations. E.g. the filter select_interior_points() requires a closed surface by default, and properties like volume assume the input is a closed surface.

Tags: filter